PAC Learnability of Scenario Decision-Making Algorithms: Necessary and Sufficient Conditions

We study the PAC property of scenario decision-making algorithms, that is, the ability to make a decision that has an arbitrarily low risk of violating an unknown safety constraint, provided sufficiently many realizations (called scenarios) of the safety constraint are sampled. Sufficient conditions for scenario decision-making algorithms to be PAC are available in the literature, such as finiteness of the VC dimension of its associated classifier and existence of a compression scheme. We study the question of whether these sufficient conditions are also necessary. We show with counterexamples that this is not the case in general. This contrasts with binary classification learning, for which the analogous conditions are sufficient and necessary. Popular scenario decision-making algorithms, such as scenario optimization, enjoy additional properties, such as stability and consistency. We show that even under these additional assumptions the above conclusions hold. Finally, we derive a necessary condition for scenario decision-making algorithms to be PAC, inspired by the VC dimension and the so-called no-free-lunch theorem.

Improved Compression Bounds for Scenario Decision Making

Scenario decision making offers a flexible way of making decision in an uncertain environment while obtaining probabilistic guarantees on the risk of failure of the decision. The idea of this approach is to draw samples of the uncertainty and make a decision based on the samples, called "scenarios". The probabilistic guarantees take the form of a bound on the probability of sampling a set of scenarios that will lead to a decision whose risk of failure is above a given maximum tolerance. This bound can be expressed as a function of the number of sampled scenarios, the maximum tolerated risk, and some intrinsic property of the problem called the "compression size". Several such bounds have been proposed in the literature under various assumptions on the problem. We propose new bounds that improve upon the existing ones without requiring stronger assumptions on the problem.

A Cantor-Kantorovich Metric Between Markov Decision Processes with Application to Transfer Learning

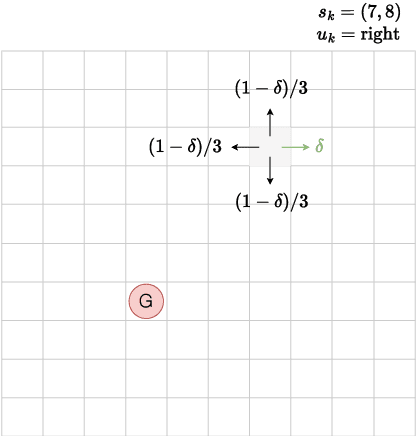
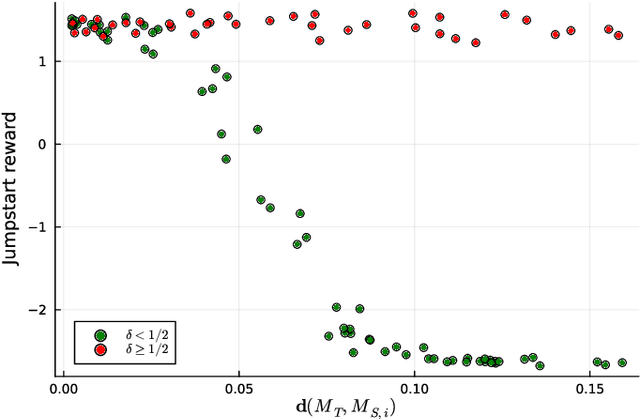
We extend the notion of Cantor-Kantorovich distance between Markov chains introduced by (Banse et al., 2023) in the context of Markov Decision Processes (MDPs). The proposed metric is well-defined and can be efficiently approximated given a finite horizon. Then, we provide numerical evidences that the latter metric can lead to interesting applications in the field of reinforcement learning. In particular, we show that it could be used for forecasting the performance of transfer learning algorithms.

Data-driven abstractions via adaptive refinements and a Kantorovich metric [extended version]

We introduce an adaptive refinement procedure for smart, and scalable abstraction of dynamical systems. Our technique relies on partitioning the state space depending on the observation of future outputs. However, this knowledge is dynamically constructed in an adaptive, asymmetric way. In order to learn the optimal structure, we define a Kantorovich-inspired metric between Markov chains, and we use it as a loss function. Our technique is prone to data-driven frameworks, but not restricted to. We also study properties of the above mentioned metric between Markov chains, which we believe could be of application for wider purpose. We propose an algorithm to approximate it, and we show that our method yields a much better computational complexity than using classical linear programming techniques.