A Cantor-Kantorovich Metric Between Markov Decision Processes with Application to Transfer Learning

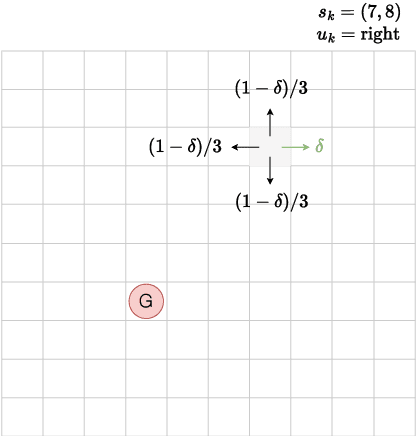
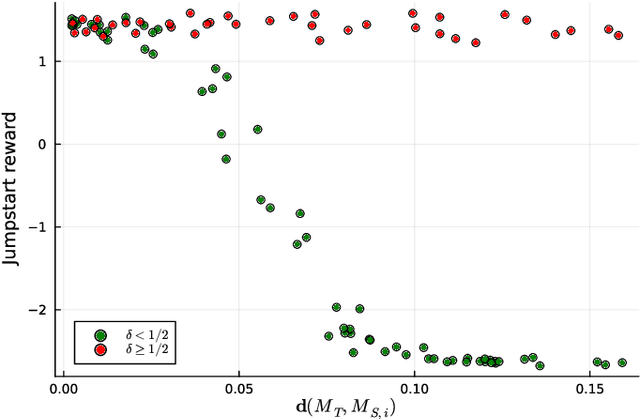
We extend the notion of Cantor-Kantorovich distance between Markov chains introduced by (Banse et al., 2023) in the context of Markov Decision Processes (MDPs). The proposed metric is well-defined and can be efficiently approximated given a finite horizon. Then, we provide numerical evidences that the latter metric can lead to interesting applications in the field of reinforcement learning. In particular, we show that it could be used for forecasting the performance of transfer learning algorithms.

Federated Learning with Differential Privacy

Federated learning (FL), as a type of distributed machine learning, is capable of significantly preserving client's private data from being shared among different parties. Nevertheless, private information can still be divulged by analyzing uploaded parameter weights from clients. In this report, we showcase our empirical benchmark of the effect of the number of clients and the addition of differential privacy (DP) mechanisms on the performance of the model on different types of data. Our results show that non-i.i.d and small datasets have the highest decrease in performance in a distributed and differentially private setting.

Data-driven abstractions via adaptive refinements and a Kantorovich metric [extended version]

We introduce an adaptive refinement procedure for smart, and scalable abstraction of dynamical systems. Our technique relies on partitioning the state space depending on the observation of future outputs. However, this knowledge is dynamically constructed in an adaptive, asymmetric way. In order to learn the optimal structure, we define a Kantorovich-inspired metric between Markov chains, and we use it as a loss function. Our technique is prone to data-driven frameworks, but not restricted to. We also study properties of the above mentioned metric between Markov chains, which we believe could be of application for wider purpose. We propose an algorithm to approximate it, and we show that our method yields a much better computational complexity than using classical linear programming techniques.