Venkata Sitaramagiridharganesh Ganapavarapu
Differentially Private Distributed Data Summarization under Covariate Shift
Oct 28, 2019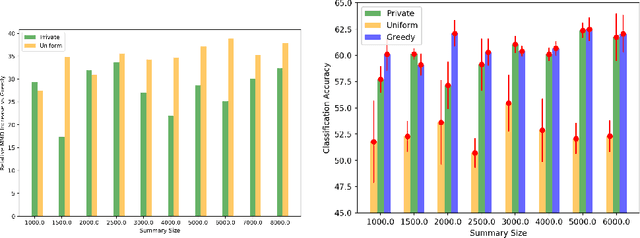
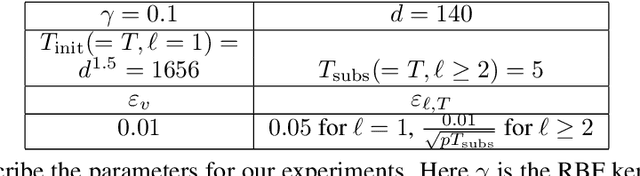
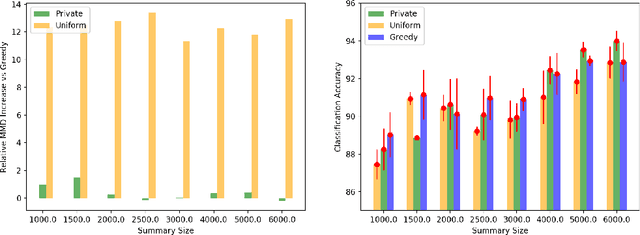
Abstract:We envision AI marketplaces to be platforms where consumers, with very less data for a target task, can obtain a relevant model by accessing many private data sources with vast number of data samples. One of the key challenges is to construct a training dataset that matches a target task without compromising on privacy of the data sources. To this end, we consider the following distributed data summarizataion problem. Given K private source datasets denoted by $[D_i]_{i\in [K]}$ and a small target validation set $D_v$, which may involve a considerable covariate shift with respect to the sources, compute a summary dataset $D_s\subseteq \bigcup_{i\in [K]} D_i$ such that its statistical distance from the validation dataset $D_v$ is minimized. We use the popular Maximum Mean Discrepancy as the measure of statistical distance. The non-private problem has received considerable attention in prior art, for example in prototype selection (Kim et al., NIPS 2016). Our work is the first to obtain strong differential privacy guarantees while ensuring the quality guarantees of the non-private version. We study this problem in a Parsimonious Curator Privacy Model, where a trusted curator coordinates the summarization process while minimizing the amount of private information accessed. Our central result is a novel protocol that (a) ensures the curator accesses at most $O(K^{\frac{1}{3}}|D_s| + |D_v|)$ points (b) has formal privacy guarantees on the leakage of information between the data owners and (c) closely matches the best known non-private greedy algorithm. Our protocol uses two hash functions, one inspired by the Rahimi-Recht random features method and the second leverages state of the art differential privacy mechanisms. We introduce a novel "noiseless" differentially private auctioning protocol for winner notification and demonstrate the efficacy of our protocol using real-world datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge