On architectural choices in deep learning: From network structure to gradient convergence and parameter estimation

We study mechanisms to characterize how the asymptotic convergence of backpropagation in deep architectures, in general, is related to the network structure, and how it may be influenced by other design choices including activation type, denoising and dropout rate. We seek to analyze whether network architecture and input data statistics may guide the choices of learning parameters and vice versa. Given the broad applicability of deep architectures, this issue is interesting both from theoretical and a practical standpoint. Using properties of general nonconvex objectives (with first-order information), we first build the association between structural, distributional and learnability aspects of the network vis-\`a-vis their interaction with parameter convergence rates. We identify a nice relationship between feature denoising and dropout, and construct families of networks that achieve the same level of convergence. We then derive a workflow that provides systematic guidance regarding the choice of network sizes and learning parameters often mediated4 by input statistics. Our technical results are corroborated by an extensive set of evaluations, presented in this paper as well as independent empirical observations reported by other groups. We also perform experiments showing the practical implications of our framework for choosing the best fully-connected design for a given problem.

On the interplay of network structure and gradient convergence in deep learning

The regularization and output consistency behavior of dropout and layer-wise pretraining for learning deep networks have been fairly well studied. However, our understanding of how the asymptotic convergence of backpropagation in deep architectures is related to the structural properties of the network and other design choices (like denoising and dropout rate) is less clear at this time. An interesting question one may ask is whether the network architecture and input data statistics may guide the choices of learning parameters and vice versa. In this work, we explore the association between such structural, distributional and learnability aspects vis-\`a-vis their interaction with parameter convergence rates. We present a framework to address these questions based on convergence of backpropagation for general nonconvex objectives using first-order information. This analysis suggests an interesting relationship between feature denoising and dropout. Building upon these results, we obtain a setup that provides systematic guidance regarding the choice of learning parameters and network sizes that achieve a certain level of convergence (in the optimization sense) often mediated by statistical attributes of the inputs. Our results are supported by a set of experimental evaluations as well as independent empirical observations reported by other groups.

Convergence of gradient based pre-training in Denoising autoencoders

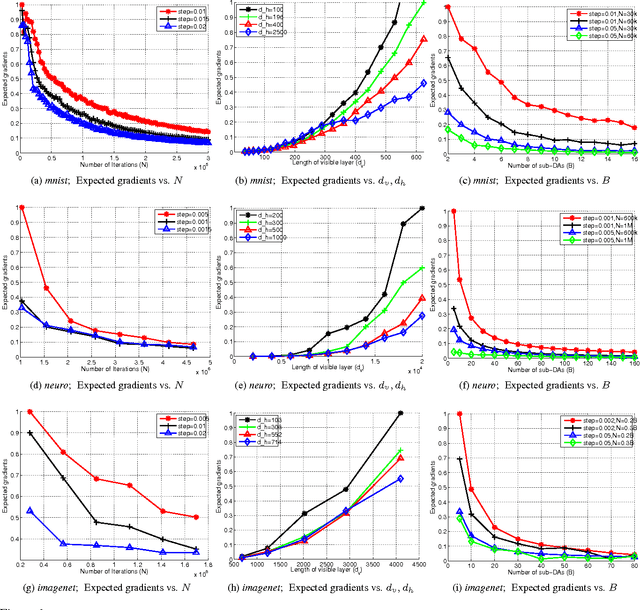
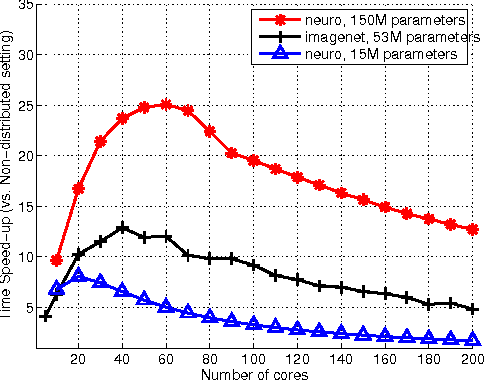
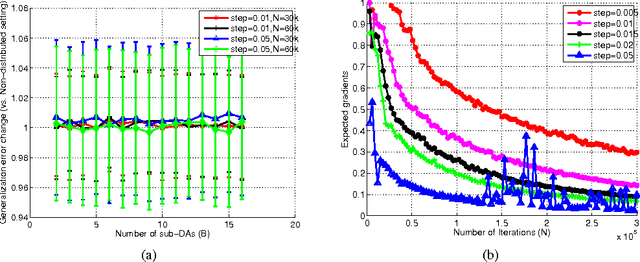
The success of deep architectures is at least in part attributed to the layer-by-layer unsupervised pre-training that initializes the network. Various papers have reported extensive empirical analysis focusing on the design and implementation of good pre-training procedures. However, an understanding pertaining to the consistency of parameter estimates, the convergence of learning procedures and the sample size estimates is still unavailable in the literature. In this work, we study pre-training in classical and distributed denoising autoencoders with these goals in mind. We show that the gradient converges at the rate of $\frac{1}{\sqrt{N}}$ and has a sub-linear dependence on the size of the autoencoder network. In a distributed setting where disjoint sections of the whole network are pre-trained synchronously, we show that the convergence improves by at least $\tau^{3/4}$, where $\tau$ corresponds to the size of the sections. We provide a broad set of experiments to empirically evaluate the suggested behavior.

Speeding up Permutation Testing in Neuroimaging

Multiple hypothesis testing is a significant problem in nearly all neuroimaging studies. In order to correct for this phenomena, we require a reliable estimate of the Family-Wise Error Rate (FWER). The well known Bonferroni correction method, while simple to implement, is quite conservative, and can substantially under-power a study because it ignores dependencies between test statistics. Permutation testing, on the other hand, is an exact, non-parametric method of estimating the FWER for a given $\alpha$-threshold, but for acceptably low thresholds the computational burden can be prohibitive. In this paper, we show that permutation testing in fact amounts to populating the columns of a very large matrix ${\bf P}$. By analyzing the spectrum of this matrix, under certain conditions, we see that ${\bf P}$ has a low-rank plus a low-variance residual decomposition which makes it suitable for highly sub--sampled --- on the order of $0.5\%$ --- matrix completion methods. Based on this observation, we propose a novel permutation testing methodology which offers a large speedup, without sacrificing the fidelity of the estimated FWER. Our evaluations on four different neuroimaging datasets show that a computational speedup factor of roughly $50\times$ can be achieved while recovering the FWER distribution up to very high accuracy. Further, we show that the estimated $\alpha$-threshold is also recovered faithfully, and is stable.