Convergence of gradient based pre-training in Denoising autoencoders
Paper and Code
Feb 12, 2015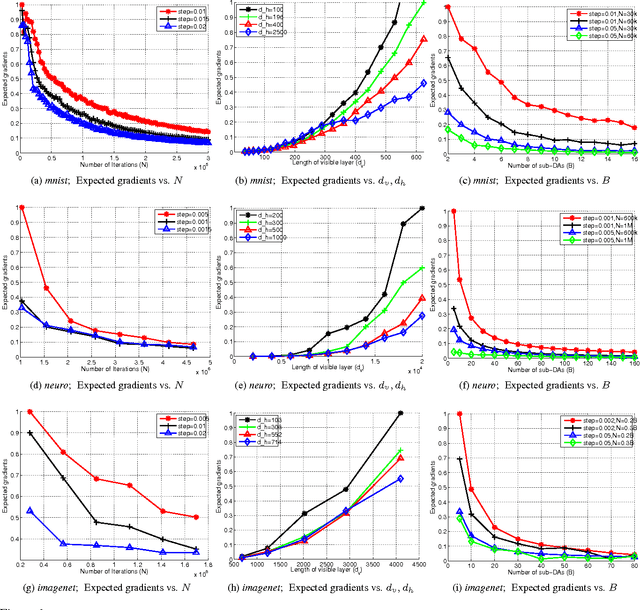
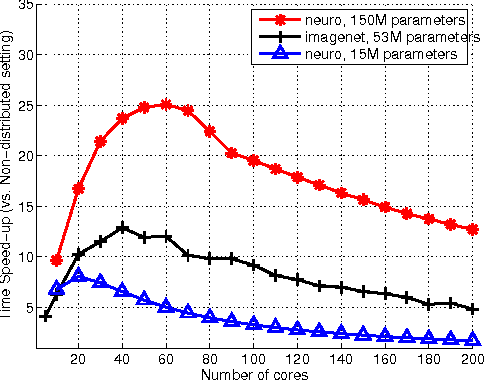
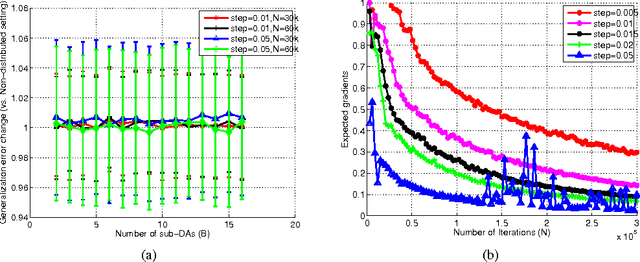
The success of deep architectures is at least in part attributed to the layer-by-layer unsupervised pre-training that initializes the network. Various papers have reported extensive empirical analysis focusing on the design and implementation of good pre-training procedures. However, an understanding pertaining to the consistency of parameter estimates, the convergence of learning procedures and the sample size estimates is still unavailable in the literature. In this work, we study pre-training in classical and distributed denoising autoencoders with these goals in mind. We show that the gradient converges at the rate of $\frac{1}{\sqrt{N}}$ and has a sub-linear dependence on the size of the autoencoder network. In a distributed setting where disjoint sections of the whole network are pre-trained synchronously, we show that the convergence improves by at least $\tau^{3/4}$, where $\tau$ corresponds to the size of the sections. We provide a broad set of experiments to empirically evaluate the suggested behavior.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge