CNNs are Myopic

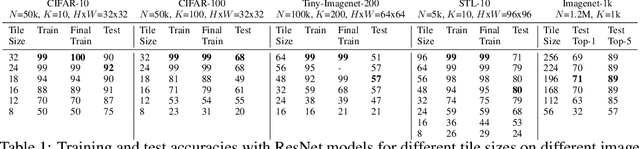
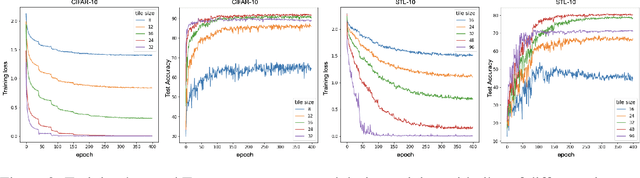
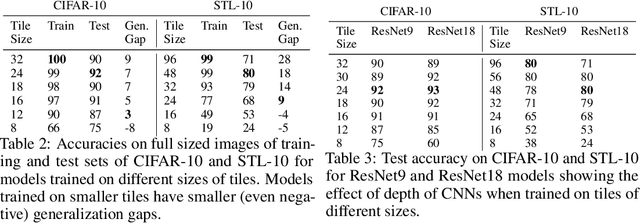
We claim that Convolutional Neural Networks (CNNs) learn to classify images using only small seemingly unrecognizable tiles. We show experimentally that CNNs trained only using such tiles can match or even surpass the performance of CNNs trained on full images. Conversely, CNNs trained on full images show similar predictions on small tiles. We also propose the first a priori theoretical model for convolutional data sets that seems to explain this behavior. This gives additional support to the long standing suspicion that CNNs do not need to understand the global structure of images to achieve state-of-the-art accuracies. Surprisingly it also suggests that over-fitting is not needed either.

Predicting Generalization in Deep Learning via Local Measures of Distortion

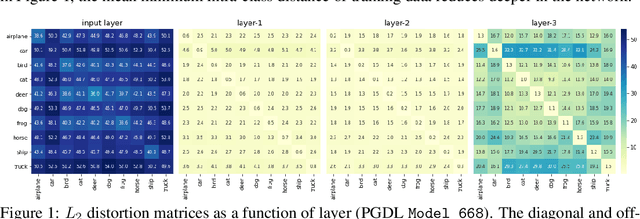
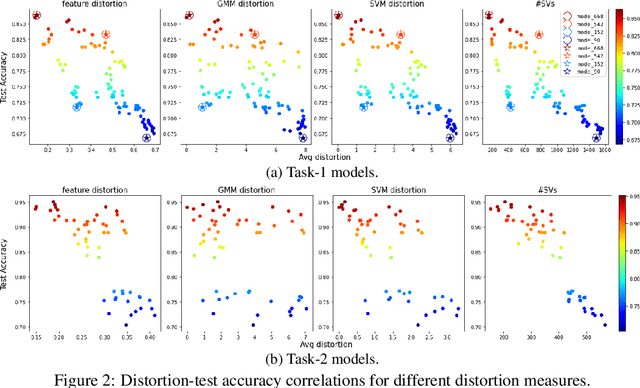
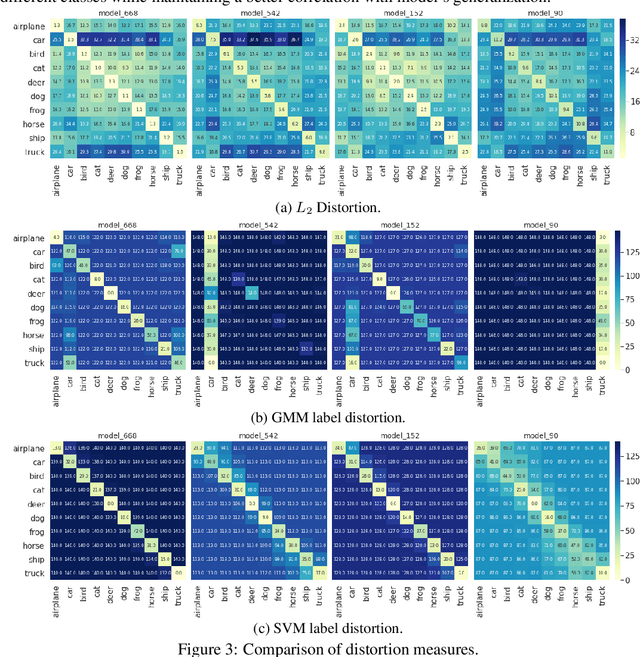
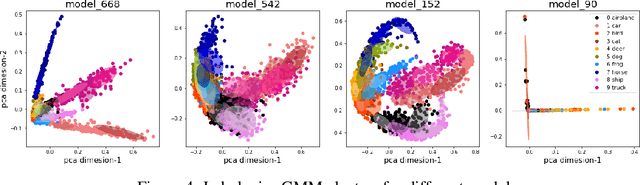
We study generalization in deep learning by appealing to complexity measures originally developed in approximation and information theory. While these concepts are challenged by the high-dimensional and data-defined nature of deep learning, we show that simple vector quantization approaches such as PCA, GMMs, and SVMs capture their spirit when applied layer-wise to deep extracted features giving rise to relatively inexpensive complexity measures that correlate well with generalization performance. We discuss our results in 2020 NeurIPS PGDL challenge.