Predicting Generalization in Deep Learning via Local Measures of Distortion
Paper and Code
Dec 16, 2020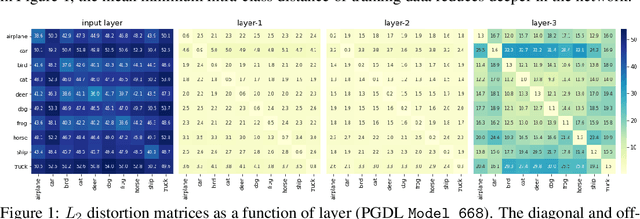
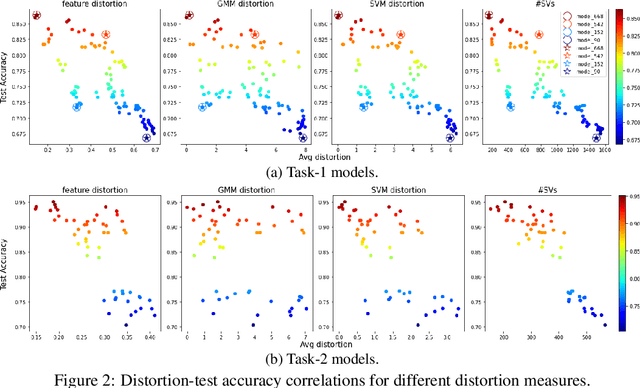
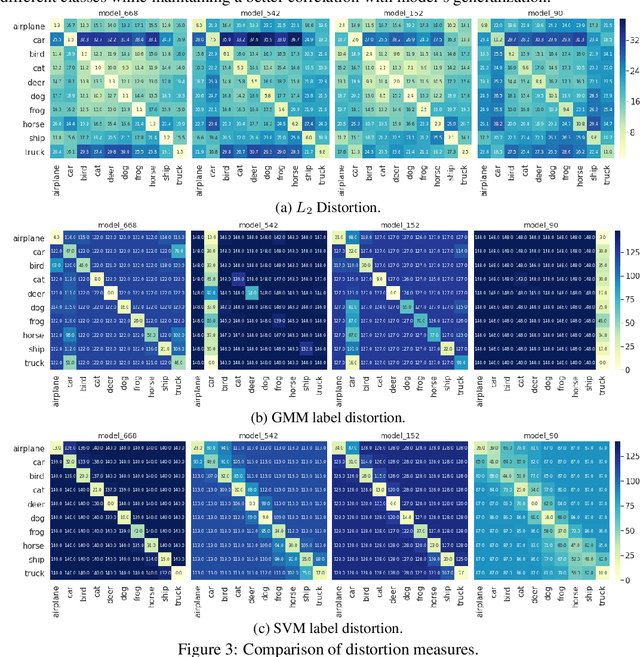
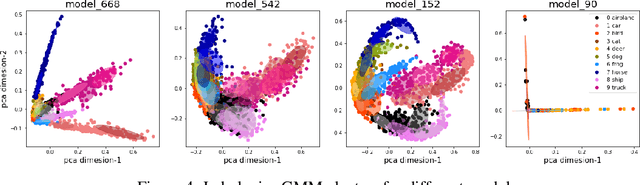
We study generalization in deep learning by appealing to complexity measures originally developed in approximation and information theory. While these concepts are challenged by the high-dimensional and data-defined nature of deep learning, we show that simple vector quantization approaches such as PCA, GMMs, and SVMs capture their spirit when applied layer-wise to deep extracted features giving rise to relatively inexpensive complexity measures that correlate well with generalization performance. We discuss our results in 2020 NeurIPS PGDL challenge.
* Added preprint footnote
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge