Valentín Osuna-Enciso
A GPU-Accelerated Moving-Horizon Algorithm for Training Deep Classification Trees on Large Datasets
Nov 12, 2023



Abstract:Decision trees are essential yet NP-complete to train, prompting the widespread use of heuristic methods such as CART, which suffers from sub-optimal performance due to its greedy nature. Recently, breakthroughs in finding optimal decision trees have emerged; however, these methods still face significant computational costs and struggle with continuous features in large-scale datasets and deep trees. To address these limitations, we introduce a moving-horizon differential evolution algorithm for classification trees with continuous features (MH-DEOCT). Our approach consists of a discrete tree decoding method that eliminates duplicated searches between adjacent samples, a GPU-accelerated implementation that significantly reduces running time, and a moving-horizon strategy that iteratively trains shallow subtrees at each node to balance the vision and optimizer capability. Comprehensive studies on 68 UCI datasets demonstrate that our approach outperforms the heuristic method CART on training and testing accuracy by an average of 3.44% and 1.71%, respectively. Moreover, these numerical studies empirically demonstrate that MH-DEOCT achieves near-optimal performance (only 0.38% and 0.06% worse than the global optimal method on training and testing, respectively), while it offers remarkable scalability for deep trees (e.g., depth=8) and large-scale datasets (e.g., ten million samples).
A Comparison of Nature Inspired Algorithms for Multi-threshold Image Segmentation
May 28, 2014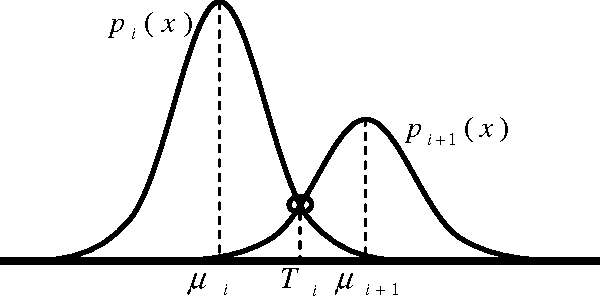
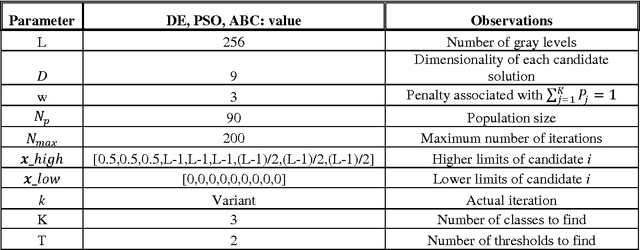

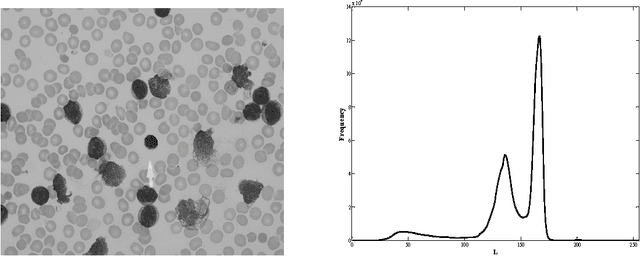
Abstract:In the field of image analysis, segmentation is one of the most important preprocessing steps. One way to achieve segmentation is by mean of threshold selection, where each pixel that belongs to a determined class islabeled according to the selected threshold, giving as a result pixel groups that share visual characteristics in the image. Several methods have been proposed in order to solve threshold selectionproblems; in this work, it is used the method based on the mixture of Gaussian functions to approximate the 1D histogram of a gray level image and whose parameters are calculated using three nature inspired algorithms (Particle Swarm Optimization, Artificial Bee Colony Optimization and Differential Evolution). Each Gaussian function approximates thehistogram, representing a pixel class and therefore a threshold point. Experimental results are shown, comparing in quantitative and qualitative fashion as well as the main advantages and drawbacks of each algorithm, applied to multi-threshold problem.
* 16 pages, this is a draft of the final version of the article sent to the Journal
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge