Knowledge-Guided Additive Modeling For Supervised Regression

Learning processes by exploiting restricted domain knowledge is an important task across a plethora of scientific areas, with more and more hybrid methods combining data-driven and model-based approaches. However, while such hybrid methods have been tested in various scientific applications, they have been mostly tested on dynamical systems, with only limited study about the influence of each model component on global performance and parameter identification. In this work, we assess the performance of hybrid modeling against traditional machine learning methods on standard regression problems. We compare, on both synthetic and real regression problems, several approaches for training such hybrid models. We focus on hybrid methods that additively combine a parametric physical term with a machine learning term and investigate model-agnostic training procedures. We also introduce a new hybrid approach based on partial dependence functions. Experiments are carried out with different types of machine learning models, including tree-based models and artificial neural networks.

Optimizing model-agnostic Random Subspace ensembles

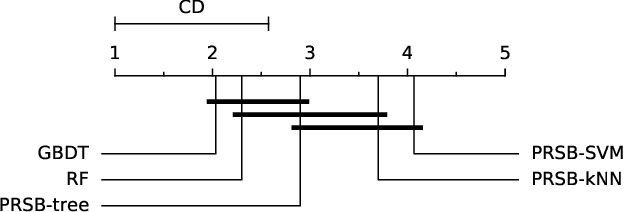
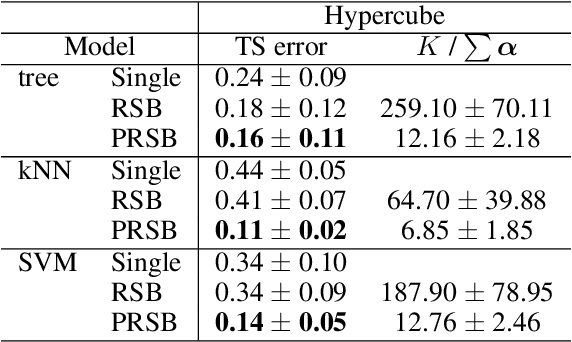
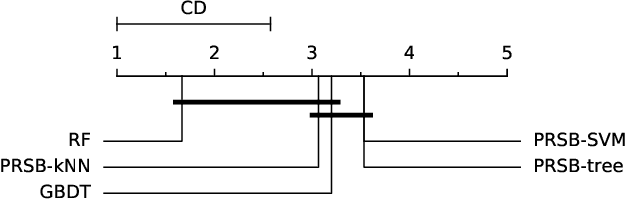
This paper presents a model-agnostic ensemble approach for supervised learning. The proposed approach alternates between (1) learning an ensemble of models using a parametric version of the Random Subspace approach, in which feature subsets are sampled according to Bernoulli distributions, and (2) identifying the parameters of the Bernoulli distributions that minimize the generalization error of the ensemble model. Parameter optimization is rendered tractable by using an importance sampling approach able to estimate the expected model output for any given parameter set, without the need to learn new models. While the degree of randomization is controlled by a hyper-parameter in standard Random Subspace, it has the advantage to be automatically tuned in our parametric version. Furthermore, model-agnostic feature importance scores can be easily derived from the trained ensemble model. We show the good performance of the proposed approach, both in terms of prediction and feature ranking, on simulated and real-world datasets. We also show that our approach can be successfully used for the reconstruction of gene regulatory networks.

Context-dependent feature analysis with random forests

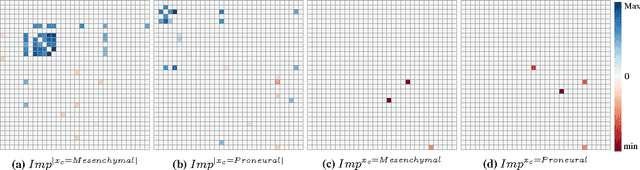
In many cases, feature selection is often more complicated than identifying a single subset of input variables that would together explain the output. There may be interactions that depend on contextual information, i.e., variables that reveal to be relevant only in some specific circumstances. In this setting, the contribution of this paper is to extend the random forest variable importances framework in order (i) to identify variables whose relevance is context-dependent and (ii) to characterize as precisely as possible the effect of contextual information on these variables. The usage and the relevance of our framework for highlighting context-dependent variables is illustrated on both artificial and real datasets.