Uriel Feige
Fair Shares: Feasibility, Domination and Incentives
May 16, 2022Abstract:We consider fair allocation of a set $M$ of indivisible goods to $n$ equally-entitled agents, with no monetary transfers. Every agent $i$ has a valuation $v_i$ from some given class of valuation functions. A share $s$ is a function that maps a pair $(v_i,n)$ to a value, with the interpretation that if an allocation of $M$ to $n$ agents fails to give agent $i$ a bundle of value at least equal to $s(v_i,n)$, this serves as evidence that the allocation is not fair towards $i$. For such an interpretation to make sense, we would like the share to be feasible, meaning that for any valuations in the class, there is an allocation that gives every agent at least her share. The maximin share was a natural candidate for a feasible share for additive valuations. However, Kurokawa, Procaccia and Wang [2018] show that it is not feasible. We initiate a systematic study of the family of feasible shares. We say that a share is \emph{self maximizing} if truth-telling maximizes the implied guarantee. We show that every feasible share is dominated by some self-maximizing and feasible share. We seek to identify those self-maximizing feasible shares that are polynomial time computable, and offer the highest share values. We show that a SM-dominating feasible share -- one that dominates every self-maximizing (SM) feasible share -- does not exist for additive valuations (and beyond). Consequently, we relax the domination property to that of domination up to a multiplicative factor of $\rho$ (called $\rho$-dominating). For additive valuations we present shares that are feasible, self-maximizing and polynomial-time computable. For $n$ agents we present such a share that is $\frac{2n}{3n-1}$-dominating. For two agents we present such a share that is $(1 - \epsilon)$-dominating. Moreover, for these shares we present poly-time algorithms that compute allocations that give every agent at least her share.
Chasing Ghosts: Competing with Stateful Policies
Jul 29, 2014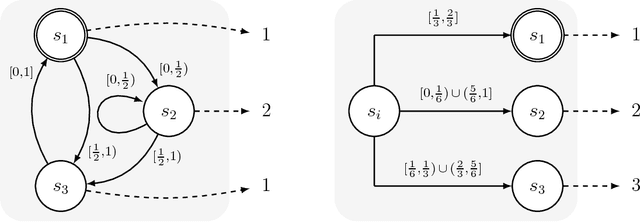
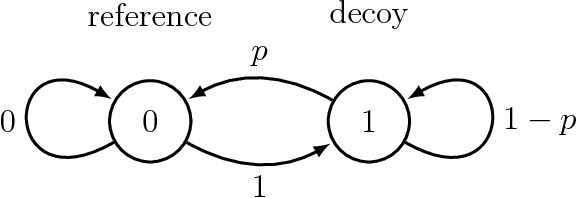

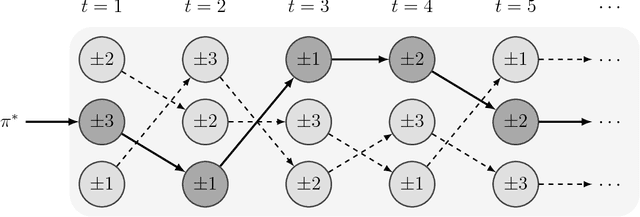
Abstract:We consider sequential decision making in a setting where regret is measured with respect to a set of stateful reference policies, and feedback is limited to observing the rewards of the actions performed (the so called "bandit" setting). If either the reference policies are stateless rather than stateful, or the feedback includes the rewards of all actions (the so called "expert" setting), previous work shows that the optimal regret grows like $\Theta(\sqrt{T})$ in terms of the number of decision rounds $T$. The difficulty in our setting is that the decision maker unavoidably loses track of the internal states of the reference policies, and thus cannot reliably attribute rewards observed in a certain round to any of the reference policies. In fact, in this setting it is impossible for the algorithm to estimate which policy gives the highest (or even approximately highest) total reward. Nevertheless, we design an algorithm that achieves expected regret that is sublinear in $T$, of the form $O( T/\log^{1/4}{T})$. Our algorithm is based on a certain local repetition lemma that may be of independent interest. We also show that no algorithm can guarantee expected regret better than $O( T/\log^{3/2} T)$.
Why are images smooth?
Jun 19, 2014Abstract:It is a well observed phenomenon that natural images are smooth, in the sense that nearby pixels tend to have similar values. We describe a mathematical model of images that makes no assumptions on the nature of the environment that images depict. It only assumes that images can be taken at different scales (zoom levels). We provide quantitative bounds on the smoothness of a typical image in our model, as a function of the number of available scales. These bounds can serve as a baseline against which to compare the observed smoothness of natural images.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge