Chasing Ghosts: Competing with Stateful Policies

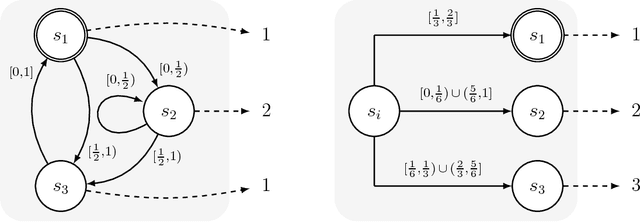
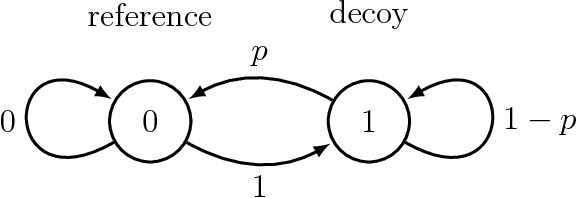
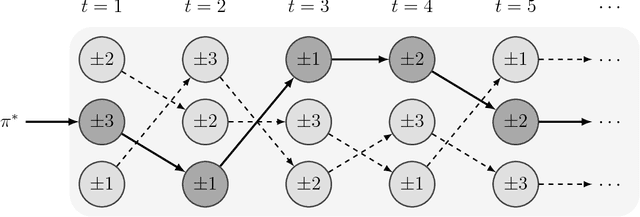
We consider sequential decision making in a setting where regret is measured with respect to a set of stateful reference policies, and feedback is limited to observing the rewards of the actions performed (the so called "bandit" setting). If either the reference policies are stateless rather than stateful, or the feedback includes the rewards of all actions (the so called "expert" setting), previous work shows that the optimal regret grows like $\Theta(\sqrt{T})$ in terms of the number of decision rounds $T$. The difficulty in our setting is that the decision maker unavoidably loses track of the internal states of the reference policies, and thus cannot reliably attribute rewards observed in a certain round to any of the reference policies. In fact, in this setting it is impossible for the algorithm to estimate which policy gives the highest (or even approximately highest) total reward. Nevertheless, we design an algorithm that achieves expected regret that is sublinear in $T$, of the form $O( T/\log^{1/4}{T})$. Our algorithm is based on a certain local repetition lemma that may be of independent interest. We also show that no algorithm can guarantee expected regret better than $O( T/\log^{3/2} T)$.