Backtracking New Q-Newton's method, Newton's flow, Voronoi's diagram and Stochastic root finding

A new variant of Newton's method - named Backtracking New Q-Newton's method (BNQN) - which has strong theoretical guarantee, is easy to implement, and has good experimental performance, was recently introduced by the third author. Experiments performed previously showed some remarkable properties of the basins of attractions for finding roots of polynomials and meromorphic functions, with BNQN. In general, they look more smooth than that of Newton's method. In this paper, we continue to experimentally explore in depth this remarkable phenomenon, and connect BNQN to Newton's flow and Voronoi's diagram. This link poses a couple of challenging puzzles to be explained. Experiments also indicate that BNQN is more robust against random perturbations than Newton's method and Random Relaxed Newton's method.

Creating walls to avoid unwanted points in root finding and optimization

In root finding and optimization, there are many cases where there is a closed set $A$ one likes that the sequence constructed by one's favourite method will not converge to A (here, we do not assume extra properties on $A$ such as being convex or connected). For example, if one wants to find roots, and one chooses initial points in the basin of attraction for 1 root $x^*$ (a fact which one may not know before hand), then one will always end up in that root. In this case, one would like to have a mechanism to avoid this point $z^*$ in the next runs of one's algorithm. In this paper, we propose two new methods aiming to achieve this. In the first method, we divide the cost function by an appropriate power of the distance function to $A$. This idea is inspired by how one would try to find all roots of a function in 1 variable. In the second method, which is more suitable for constrained optimization, we redefine the value of the function to be a big constant on $A$. We also propose, based on this, an algorithm to escape the basin of attraction of a component of positive dimension to reach another component. As an application, we prove a rigorous guarantee for finding roots of a meromorphic function of 1 complex variable in a given domain. Along the way, we compare with main existing relevant methods in the current literature. We provide several examples in various different settings to illustrate the usefulness of the new approach.

CapillaryX: A Software Design Pattern for Analyzing Medical Images in Real-time using Deep Learning

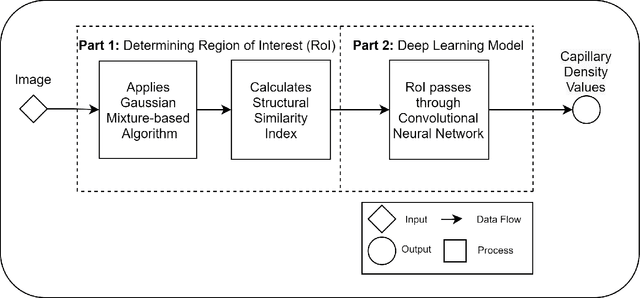
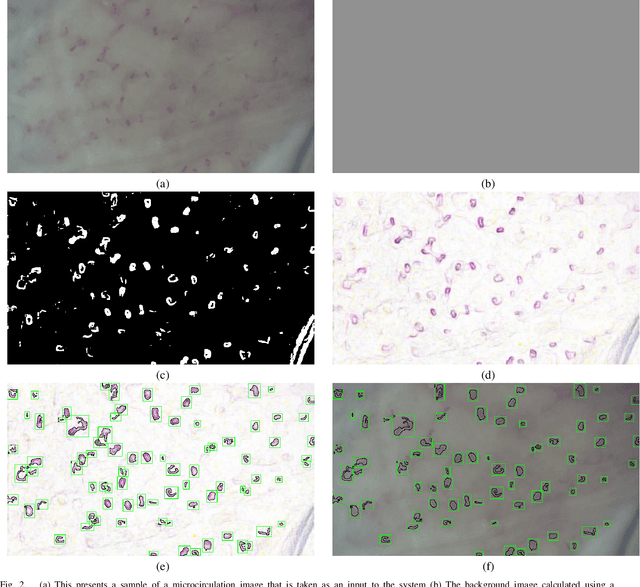
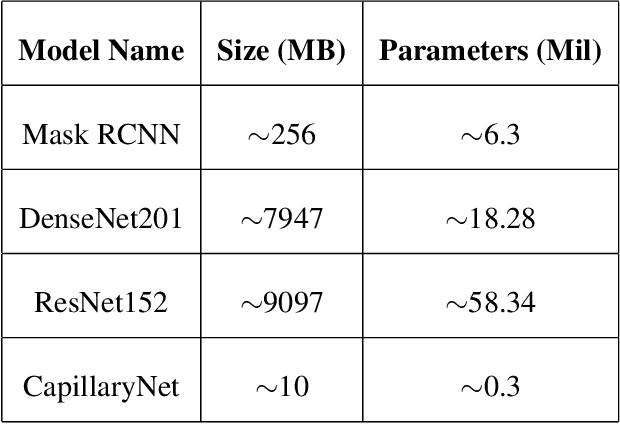
Recent advances in digital imaging, e.g., increased number of pixels captured, have meant that the volume of data to be processed and analyzed from these images has also increased. Deep learning algorithms are state-of-the-art for analyzing such images, given their high accuracy when trained with a large data volume of data. Nevertheless, such analysis requires considerable computational power, making such algorithms time- and resource-demanding. Such high demands can be met by using third-party cloud service providers. However, analyzing medical images using such services raises several legal and privacy challenges and does not necessarily provide real-time results. This paper provides a computing architecture that locally and in parallel can analyze medical images in real-time using deep learning thus avoiding the legal and privacy challenges stemming from uploading data to a third-party cloud provider. To make local image processing efficient on modern multi-core processors, we utilize parallel execution to offset the resource-intensive demands of deep neural networks. We focus on a specific medical-industrial case study, namely the quantifying of blood vessels in microcirculation images for which we have developed a working system. It is currently used in an industrial, clinical research setting as part of an e-health application. Our results show that our system is approximately 78% faster than its serial system counterpart and 12% faster than a master-slave parallel system architecture.

Generalisations and improvements of New Q-Newton's method Backtracking

In this paper, we propose a general framework for the algorithm New Q-Newton's method Backtracking, developed in the author's previous work. For a symmetric, square real matrix $A$, we define $minsp(A):=\min _{||e||=1} ||Ae||$. Given a $C^2$ cost function $f:\mathbb{R}^m\rightarrow \mathbb{R}$ and a real number $0<\tau $, as well as $m+1$ fixed real numbers $\delta _0,\ldots ,\delta _m$, we define for each $x\in \mathbb{R}^m$ with $\nabla f(x)\not= 0$ the following quantities: $\kappa :=\min _{i\not= j}|\delta _i-\delta _j|$; $A(x):=\nabla ^2f(x)+\delta ||\nabla f(x)||^{\tau}Id$, where $\delta$ is the first element in the sequence $\{\delta _0,\ldots ,\delta _m\}$ for which $minsp(A(x))\geq \kappa ||\nabla f(x)||^{\tau}$; $e_1(x),\ldots ,e_m(x)$ are an orthonormal basis of $\mathbb{R}^m$, chosen appropriately; $w(x)=$ the step direction, given by the formula: $$w(x)=\sum _{i=1}^m\frac{<\nabla f(x),e_i(x)>}{||A(x)e_i(x)||}e_i(x);$$ (we can also normalise by $w(x)/\max \{1,||w(x)||\}$ when needed) $\gamma (x)>0$ learning rate chosen by Backtracking line search so that Armijo's condition is satisfied: $$f(x-\gamma (x)w(x))-f(x)\leq -\frac{1}{3}\gamma (x)<\nabla f(x),w(x)>.$$ The update rule for our algorithm is $x\mapsto H(x)=x-\gamma (x)w(x)$. In New Q-Newton's method Backtracking, the choices are $\tau =1+\alpha >1$ and $e_1(x),\ldots ,e_m(x)$'s are eigenvectors of $\nabla ^2f(x)$. In this paper, we allow more flexibility and generality, for example $\tau$ can be chosen to be $<1$ or $e_1(x),\ldots ,e_m(x)$'s are not necessarily eigenvectors of $\nabla ^2f(x)$. New Q-Newton's method Backtracking (as well as Backtracking gradient descent) is a special case, and some versions have flavours of quasi-Newton's methods. Several versions allow good theoretical guarantees. An application to solving systems of polynomial equations is given.

New Q-Newton's method meets Backtracking line search: good convergence guarantee, saddle points avoidance, quadratic rate of convergence, and easy implementation

In a recent joint work, the author has developed a modification of Newton's method, named New Q-Newton's method, which can avoid saddle points and has quadratic rate of convergence. While good theoretical convergence guarantee has not been established for this method, experiments on small scale problems show that the method works very competitively against other well known modifications of Newton's method such as Adaptive Cubic Regularization and BFGS, as well as first order methods such as Unbounded Two-way Backtracking Gradient Descent. In this paper, we resolve the convergence guarantee issue by proposing a modification of New Q-Newton's method, named New Q-Newton's method Backtracking, which incorporates a more sophisticated use of hyperparameters and a Backtracking line search. This new method has very good theoretical guarantees, which for a {\bf Morse function} yields the following (which is unknown for New Q-Newton's method): {\bf Theorem.} Let $f:\mathbb{R}^m\rightarrow \mathbb{R}$ be a Morse function, that is all its critical points have invertible Hessian. Then for a sequence $\{x_n\}$ constructed by New Q-Newton's method Backtracking from a random initial point $x_0$, we have the following two alternatives: i) $\lim _{n\rightarrow\infty}||x_n||=\infty$, or ii) $\{x_n\}$ converges to a point $x_{\infty}$ which is a {\bf local minimum} of $f$, and the rate of convergence is {\bf quadratic}. Moreover, if $f$ has compact sublevels, then only case ii) happens. As far as we know, for Morse functions, this is the best theoretical guarantee for iterative optimization algorithms so far in the literature. We have tested in experiments on small scale, with some further simplified versions of New Q-Newton's method Backtracking, and found that the new method significantly improve New Q-Newton's method.

CapillaryNet: An Automated System to Analyze Microcirculation Videos from Handheld Vital Microscopy

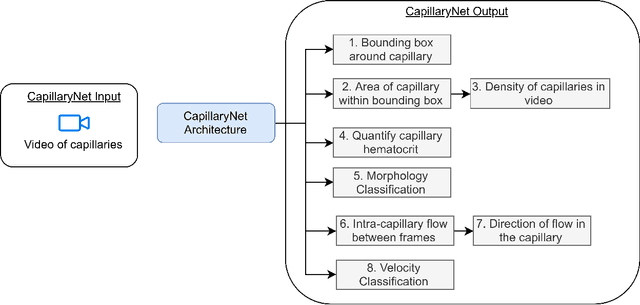
Capillaries are the smallest vessels in the body responsible for the delivery of oxygen and nutrients to the surrounding cells. Various diseases have been shown to alter the density of nutritive capillaries and the flow velocity of erythrocytes. In previous studies, capillary density and flow velocity have been assessed manually by trained specialists. Manual analysis of a 20-second long microvascular video takes on average 20 minutes and requires extensive training. Several studies have reported that manual analysis hinders the application of microvascular microscopy in a clinical setting. In this paper, we present a fully automated system, called CapillaryNet, that can automate microvascular microscopy analysis so it can be used as a clinical application. Moreover, CapillaryNet measures several microvascular parameters that researchers were previously unable to quantify, i.e. capillary hematocrit and intra-capillary flow velocity heterogeneity.

Unconstrained optimisation on Riemannian manifolds

In this paper, we give explicit descriptions of versions of (Local-) Backtracking Gradient Descent and New Q-Newton's method to the Riemannian setting.Here are some easy to state consequences of results in this paper, where X is a general Riemannian manifold of finite dimension and $f:X\rightarrow \mathbb{R}$ a $C^2$ function which is Morse (that is, all its critical points are non-degenerate). {\bf Theorem.} For random choices of the hyperparameters in the Riemanian Local Backtracking Gradient Descent algorithm and for random choices of the initial point $x_0$, the sequence $\{x_n\}$ constructed by the algorithm either (i) converges to a local minimum of $f$ or (ii) eventually leaves every compact subsets of $X$ (in other words, diverges to infinity on $X$). If $f$ has compact sublevels, then only the former alternative happens. The convergence rate is the same as in the classical paper by Armijo. {\bf Theorem.} Assume that $f$ is $C^3$. For random choices of the hyperparametes in the Riemannian New Q-Newton's method, if the sequence constructed by the algorithm converges, then the limit is a critical point of $f$. We have a local Stable-Center manifold theorem, near saddle points of $f$, for the dynamical system associated to the algorithm. If the limit point is a non-degenerate minimum point, then the rate of convergence is quadratic. If moreover $X$ is an open subset of a Lie group and the initial point $x_0$ is chosen randomly, then we can globally avoid saddle points. As an application, we propose a general method using Riemannian Backtracking GD to find minimum of a function on a bounded ball in a Euclidean space, and do explicit calculations for calculating the smallest eigenvalue of a symmetric square matrix.

Asymptotic behaviour of learning rates in Armijo's condition

Fix a constant $0<\alpha <1$. For a $C^1$ function $f:\mathbb{R}^k\rightarrow \mathbb{R}$, a point $x$ and a positive number $\delta >0$, we say that Armijo's condition is satisfied if $f(x-\delta \nabla f(x))-f(x)\leq -\alpha \delta ||\nabla f(x)||^2$. It is a basis for the well known Backtracking Gradient Descent (Backtracking GD) algorithm. Consider a sequence $\{x_n\}$ defined by $x_{n+1}=x_n-\delta _n\nabla f(x_n)$, for positive numbers $\delta _n$ for which Armijo's condition is satisfied. We show that if $\{x_n\}$ converges to a non-degenerate critical point, then $\{\delta _n\}$ must be bounded. Moreover this boundedness can be quantified in terms of the norms of the Hessian $\nabla ^2f$ and its inverse at the limit point. This complements the first author's results on Unbounded Backtracking GD, and shows that in case of convergence to a non-degenerate critical point the behaviour of Unbounded Backtracking GD is not too different from that of usual Backtracking GD. On the other hand, in case of convergence to a degenerate critical point the behaviours can be very much different. We run some experiments to illustrate that both scenrios can really happen. In another part of the paper, we argue that Backtracking GD has the correct unit (according to a definition by Zeiler in his Adadelta's paper). The main point is that since learning rate in Backtracking GD is bound by Armijo's condition, it is not unitless.

A modification of quasi-Newton's methods helping to avoid saddle points

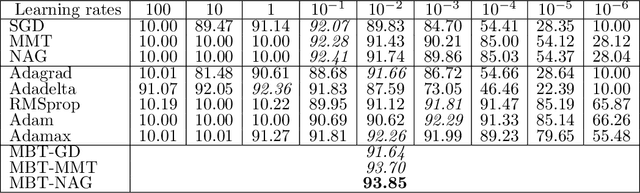
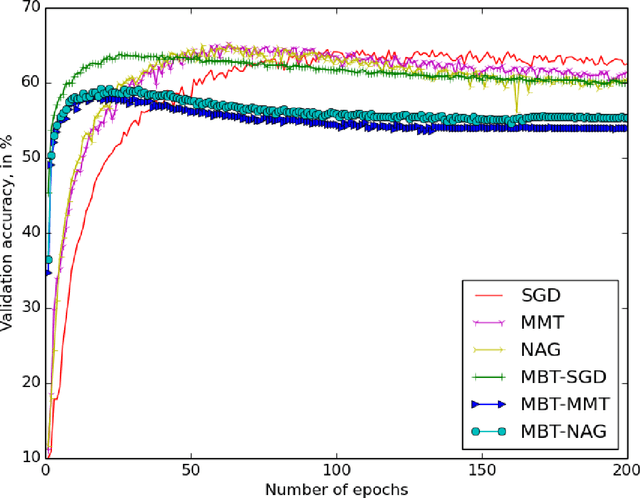
We recall that if $A$ is an invertible and symmetric real $m\times m$ matrix, then it is diagonalisable. Therefore, if we denote by $\mathcal{E}^{+}(A)\subset \mathbb{R}^m$ (respectively $\mathcal{E}^{-}(A)\subset \mathbb{R}^m$) to be the vector subspace generated by eigenvectors with positive eigenvalues of $A$ (correspondingly the vector subspace generated by eigenvectors with negative eigenvalues of $A$), then we have an orthogonal decomposition $\mathbb{R}^m=\mathcal{E}^{+}(A)\oplus \mathcal{E}^{-}(A)$. Hence, every $x\in \mathbb{R}^m$ can be written uniquely as $x=pr_{A,+}(x)+pr_{A,-}(x)$ with $pr_{A,+}(x)\in \mathcal{E}^{+}(A)$ and $pr_{A,-}(x)\in \mathcal{E}^{-}(A)$. We propose the following simple new modification of quasi-Newton's methods. {\bf New Q-Newton's method.} Let $\Delta =\{\delta _0,\delta _1,\delta _2,\ldots \}$ be a countable set of real numbers which has at least $m+1$ elements. Let $f:\mathbb{R}^m\rightarrow \mathbb{R}$ be a $C^2$ function. Let $\alpha >0$. For each $x\in \mathbb{R}^m$ such that $\nabla f(x)\not=0$, let $\delta (x)=\delta _j$, where $j$ is the smallest number so that $\nabla ^2f(x)+\delta _j||\nabla f(x)||^{1+\alpha}Id$ is invertible. (If $\nabla f(x)=0$, then we choose $\delta (x)=\delta _0$.) Let $x_0\in \mathbb{R}^m$ be an initial point. We define a sequence of $x_n\in \mathbb{R}^m$ and invertible and symmetric $m\times m$ matrices $A_n$ as follows: $A_n=\nabla ^2f(x_n)+\delta (x_n) ||\nabla f(x_n)||^{1+\alpha}Id$ and $x_{n+1}=x_n-w_n$, where $w_n=pr_{A_n,+}(v_n)-pr_{A_n,-}(v_n)$ and $v_n=A_n^{-1}\nabla f(x_n)$. The main result of this paper roughly says that if $f$ is $C^3$ and a sequence $\{x_n\}$, constructed by the New Q-Newton's method from a random initial point $x_0$, {\bf converges}, then the limit point is not a saddle point, and the convergence rate is the same as that of Newton's method.

Coordinate-wise Armijo's condition: General case

Let $z=(x,y)$ be coordinates for the product space $\mathbb{R}^{m_1}\times \mathbb{R}^{m_2}$. Let $f:\mathbb{R}^{m_1}\times \mathbb{R}^{m_2}\rightarrow \mathbb{R}$ be a $C^1$ function, and $\nabla f=(\partial _xf,\partial _yf)$ its gradient. Fix $0<\alpha <1$. For a point $(x,y) \in \mathbb{R}^{m_1}\times \mathbb{R}^{m_2}$, a number $\delta >0$ satisfies Armijo's condition at $(x,y)$ if the following inequality holds: \begin{eqnarray*} f(x-\delta \partial _xf,y-\delta \partial _yf)-f(x,y)\leq -\alpha \delta (||\partial _xf||^2+||\partial _yf||^2). \end{eqnarray*} In one previous paper, we proposed the following {\bf coordinate-wise} Armijo's condition. Fix again $0<\alpha <1$. A pair of positive numbers $\delta _1,\delta _2>0$ satisfies the coordinate-wise variant of Armijo's condition at $(x,y)$ if the following inequality holds: \begin{eqnarray*} [f(x-\delta _1\partial _xf(x,y), y-\delta _2\partial _y f(x,y))]-[f(x,y)]\leq -\alpha (\delta _1||\partial _xf(x,y)||^2+\delta _2||\partial _yf(x,y)||^2). \end{eqnarray*} Previously we applied this condition for functions of the form $f(x,y)=f(x)+g(y)$, and proved various convergent results for them. For a general function, it is crucial - for being able to do real computations - to have a systematic algorithm for obtaining $\delta _1$ and $\delta _2$ satisfying the coordinate-wise version of Armijo's condition, much like Backtracking for the usual Armijo's condition. In this paper we propose such an algorithm, and prove according convergent results. We then analyse and present experimental results for some functions such as $f(x,y)=a|x|+y$ (given by Asl and Overton in connection to Wolfe's method), $f(x,y)=x^3 sin (1/x) + y^3 sin(1/y)$ and Rosenbrock's function.