CapillaryNet: An Automated System to Analyze Microcirculation Videos from Handheld Vital Microscopy

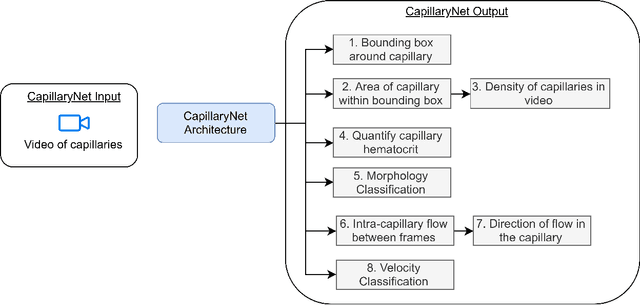
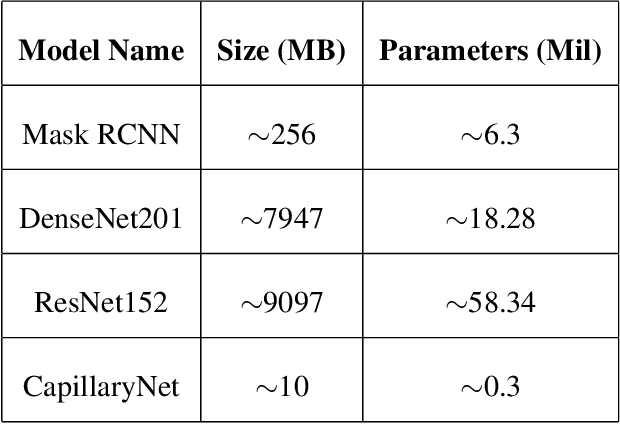
Capillaries are the smallest vessels in the body responsible for the delivery of oxygen and nutrients to the surrounding cells. Various diseases have been shown to alter the density of nutritive capillaries and the flow velocity of erythrocytes. In previous studies, capillary density and flow velocity have been assessed manually by trained specialists. Manual analysis of a 20-second long microvascular video takes on average 20 minutes and requires extensive training. Several studies have reported that manual analysis hinders the application of microvascular microscopy in a clinical setting. In this paper, we present a fully automated system, called CapillaryNet, that can automate microvascular microscopy analysis so it can be used as a clinical application. Moreover, CapillaryNet measures several microvascular parameters that researchers were previously unable to quantify, i.e. capillary hematocrit and intra-capillary flow velocity heterogeneity.

A modification of quasi-Newton's methods helping to avoid saddle points

We recall that if $A$ is an invertible and symmetric real $m\times m$ matrix, then it is diagonalisable. Therefore, if we denote by $\mathcal{E}^{+}(A)\subset \mathbb{R}^m$ (respectively $\mathcal{E}^{-}(A)\subset \mathbb{R}^m$) to be the vector subspace generated by eigenvectors with positive eigenvalues of $A$ (correspondingly the vector subspace generated by eigenvectors with negative eigenvalues of $A$), then we have an orthogonal decomposition $\mathbb{R}^m=\mathcal{E}^{+}(A)\oplus \mathcal{E}^{-}(A)$. Hence, every $x\in \mathbb{R}^m$ can be written uniquely as $x=pr_{A,+}(x)+pr_{A,-}(x)$ with $pr_{A,+}(x)\in \mathcal{E}^{+}(A)$ and $pr_{A,-}(x)\in \mathcal{E}^{-}(A)$. We propose the following simple new modification of quasi-Newton's methods. {\bf New Q-Newton's method.} Let $\Delta =\{\delta _0,\delta _1,\delta _2,\ldots \}$ be a countable set of real numbers which has at least $m+1$ elements. Let $f:\mathbb{R}^m\rightarrow \mathbb{R}$ be a $C^2$ function. Let $\alpha >0$. For each $x\in \mathbb{R}^m$ such that $\nabla f(x)\not=0$, let $\delta (x)=\delta _j$, where $j$ is the smallest number so that $\nabla ^2f(x)+\delta _j||\nabla f(x)||^{1+\alpha}Id$ is invertible. (If $\nabla f(x)=0$, then we choose $\delta (x)=\delta _0$.) Let $x_0\in \mathbb{R}^m$ be an initial point. We define a sequence of $x_n\in \mathbb{R}^m$ and invertible and symmetric $m\times m$ matrices $A_n$ as follows: $A_n=\nabla ^2f(x_n)+\delta (x_n) ||\nabla f(x_n)||^{1+\alpha}Id$ and $x_{n+1}=x_n-w_n$, where $w_n=pr_{A_n,+}(v_n)-pr_{A_n,-}(v_n)$ and $v_n=A_n^{-1}\nabla f(x_n)$. The main result of this paper roughly says that if $f$ is $C^3$ and a sequence $\{x_n\}$, constructed by the New Q-Newton's method from a random initial point $x_0$, {\bf converges}, then the limit point is not a saddle point, and the convergence rate is the same as that of Newton's method.