Asymptotic behaviour of learning rates in Armijo's condition

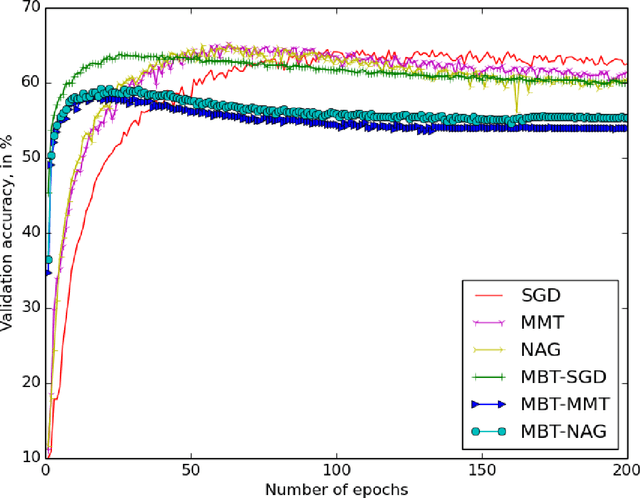
Fix a constant $0<\alpha <1$. For a $C^1$ function $f:\mathbb{R}^k\rightarrow \mathbb{R}$, a point $x$ and a positive number $\delta >0$, we say that Armijo's condition is satisfied if $f(x-\delta \nabla f(x))-f(x)\leq -\alpha \delta ||\nabla f(x)||^2$. It is a basis for the well known Backtracking Gradient Descent (Backtracking GD) algorithm. Consider a sequence $\{x_n\}$ defined by $x_{n+1}=x_n-\delta _n\nabla f(x_n)$, for positive numbers $\delta _n$ for which Armijo's condition is satisfied. We show that if $\{x_n\}$ converges to a non-degenerate critical point, then $\{\delta _n\}$ must be bounded. Moreover this boundedness can be quantified in terms of the norms of the Hessian $\nabla ^2f$ and its inverse at the limit point. This complements the first author's results on Unbounded Backtracking GD, and shows that in case of convergence to a non-degenerate critical point the behaviour of Unbounded Backtracking GD is not too different from that of usual Backtracking GD. On the other hand, in case of convergence to a degenerate critical point the behaviours can be very much different. We run some experiments to illustrate that both scenrios can really happen. In another part of the paper, we argue that Backtracking GD has the correct unit (according to a definition by Zeiler in his Adadelta's paper). The main point is that since learning rate in Backtracking GD is bound by Armijo's condition, it is not unitless.

A modification of quasi-Newton's methods helping to avoid saddle points

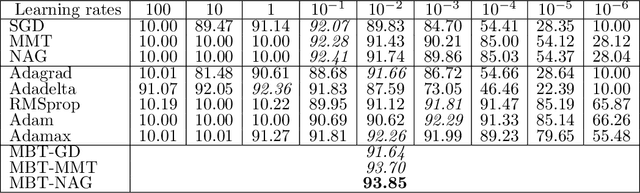
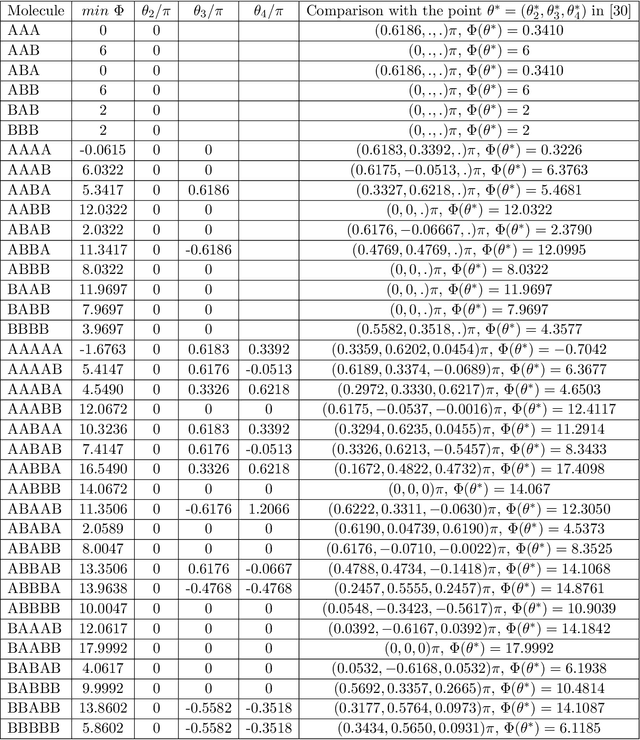
We recall that if $A$ is an invertible and symmetric real $m\times m$ matrix, then it is diagonalisable. Therefore, if we denote by $\mathcal{E}^{+}(A)\subset \mathbb{R}^m$ (respectively $\mathcal{E}^{-}(A)\subset \mathbb{R}^m$) to be the vector subspace generated by eigenvectors with positive eigenvalues of $A$ (correspondingly the vector subspace generated by eigenvectors with negative eigenvalues of $A$), then we have an orthogonal decomposition $\mathbb{R}^m=\mathcal{E}^{+}(A)\oplus \mathcal{E}^{-}(A)$. Hence, every $x\in \mathbb{R}^m$ can be written uniquely as $x=pr_{A,+}(x)+pr_{A,-}(x)$ with $pr_{A,+}(x)\in \mathcal{E}^{+}(A)$ and $pr_{A,-}(x)\in \mathcal{E}^{-}(A)$. We propose the following simple new modification of quasi-Newton's methods. {\bf New Q-Newton's method.} Let $\Delta =\{\delta _0,\delta _1,\delta _2,\ldots \}$ be a countable set of real numbers which has at least $m+1$ elements. Let $f:\mathbb{R}^m\rightarrow \mathbb{R}$ be a $C^2$ function. Let $\alpha >0$. For each $x\in \mathbb{R}^m$ such that $\nabla f(x)\not=0$, let $\delta (x)=\delta _j$, where $j$ is the smallest number so that $\nabla ^2f(x)+\delta _j||\nabla f(x)||^{1+\alpha}Id$ is invertible. (If $\nabla f(x)=0$, then we choose $\delta (x)=\delta _0$.) Let $x_0\in \mathbb{R}^m$ be an initial point. We define a sequence of $x_n\in \mathbb{R}^m$ and invertible and symmetric $m\times m$ matrices $A_n$ as follows: $A_n=\nabla ^2f(x_n)+\delta (x_n) ||\nabla f(x_n)||^{1+\alpha}Id$ and $x_{n+1}=x_n-w_n$, where $w_n=pr_{A_n,+}(v_n)-pr_{A_n,-}(v_n)$ and $v_n=A_n^{-1}\nabla f(x_n)$. The main result of this paper roughly says that if $f$ is $C^3$ and a sequence $\{x_n\}$, constructed by the New Q-Newton's method from a random initial point $x_0$, {\bf converges}, then the limit point is not a saddle point, and the convergence rate is the same as that of Newton's method.