Statistical Analysis of Target Parameter Estimation Using Passive Radar

A passive radar system uses one or more so-called Illuminators of Opportunity (IO) to detect and localize targets. In such systems, a reference channel is often used at each receiving node to capture the transmitted IO signal, while targets are detected using the main surveillance channel. The purpose of the present contribution is to analyze a method for estimating the target parameters in such a system. Specifically, we quantify the additional error contribution due to not knowing the transmitted IO waveform perfectly. A sufficient condition for this error to be negligible as compared to errors due to clutter and noise in the surveillance channel is then given.

Analysis of Interpolating Regression Models and the Double Descent Phenomenon

A regression model with more parameters than data points in the training data is overparametrized and has the capability to interpolate the training data. Based on the classical bias-variance tradeoff expressions, it is commonly assumed that models which interpolate noisy training data are poor to generalize. In some cases, this is not true. The best models obtained are overparametrized and the testing error exhibits the double descent behavior as the model order increases. In this contribution, we provide some analysis to explain the double descent phenomenon, first reported in the machine learning literature. We focus on interpolating models derived from the minimum norm solution to the classical least-squares problem and also briefly discuss model fitting using ridge regression. We derive a result based on the behavior of the smallest singular value of the regression matrix that explains the peak location and the double descent shape of the testing error as a function of model order.

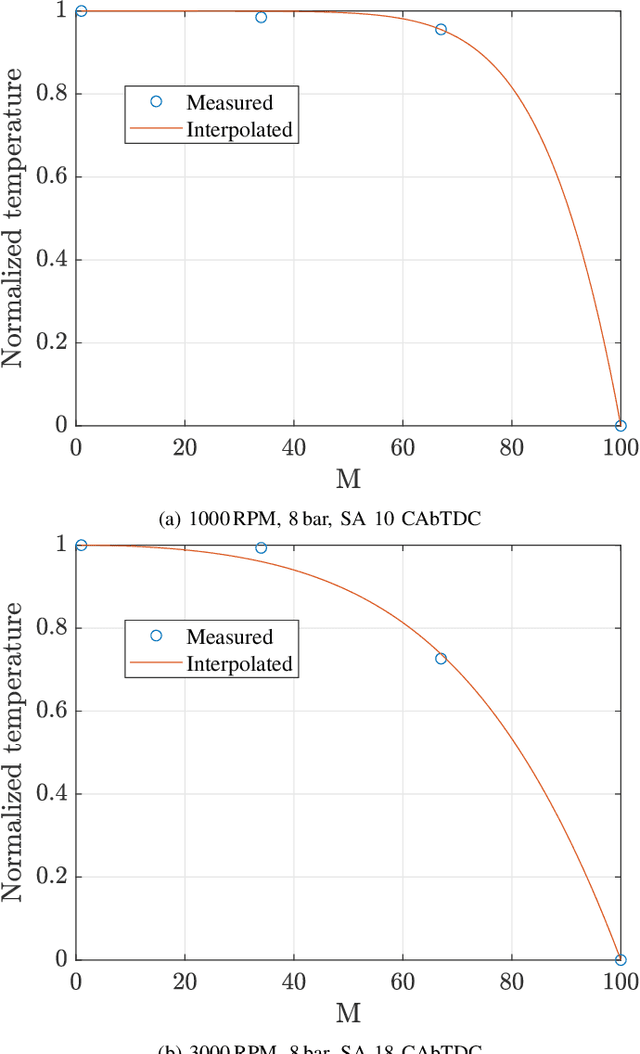
Cold-Start Modeling and On-Line Optimal Control of the Three-Way Catalyst

We present a three-way catalyst (TWC) cold-start model, calibrate the model based on experimental data from multiple operating points, and use the model to generate a Pareto-optimal cold-start controller suitable for implementation in standard engine control unit hardware. The TWC model is an extension of a previously presented physics-based model that predicts carbon monoxide, hydrocarbon, and nitrogen oxides tailpipe emissions. The model axially and radially resolves the temperatures in the monolith using very few state variables, thus allowing for use with control-policy based optimal control methods. In this paper we extend the model to allow for variable axial discretization lengths, include the heat of reaction from hydrogen gas generated from the combustion engine, and reformulate the model parameters to be expressed in conventional units. We experimentally measured the temperature and emission evolution for cold-starts with ten different engine load points, which was subsequently used to tune the model parameters (e.g.~chemical reaction rates, specific heats, and thermal resistances). The simulated cumulative tailpipe emission modeling error was found to be typically -20% to +80% of the measured emissions. We have constructed and simulated the performance of a Pareto-optimal controller using this model that balances fuel efficiency and the cumulative emissions of each individual species. A benchmark of the optimal controller with a conventional cold-start strategy shows the potential for reducing the cold-start emissions.

Separable Convolutional Eigen-Filters (SCEF): Building Efficient CNNs Using Redundancy Analysis

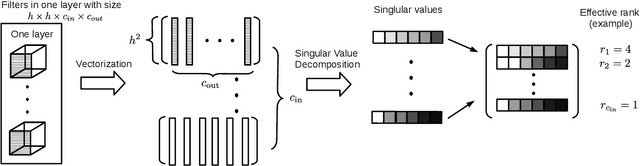
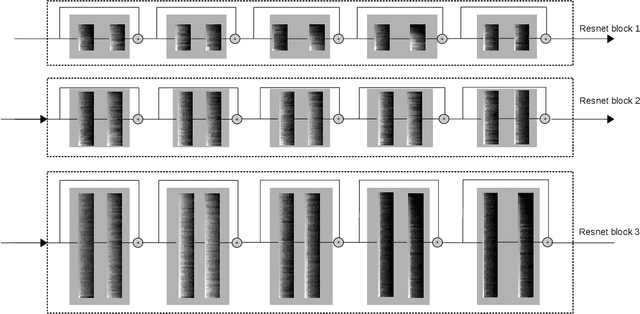
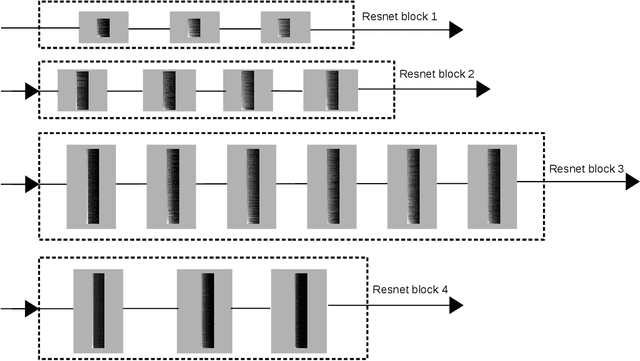
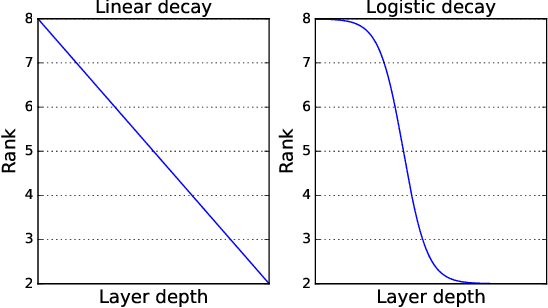
Deep Convolutional Neural Networks (CNNs) have been widely used in computer vision due to its effectiveness. While the high model complexity of CNN enables remarkable learning capacity, the large number of trainable parameters comes with a high cost. In addition to the demand of a large amount of resources, the high complexity of the network can result in a high variance in its generalization performance from a statistical learning theory perspective. One way to reduce the complexity of a network without sacrificing its accuracy is to define and identify redundancies in order to remove them. In this work, we propose a method to observe and analyze redundancies in the weights of 2D convolutional (Conv2D) filters. From our experiments, we observe that 1) the vectorized Conv2D filters exhibit low rank behaviors; 2) the effective ranks of these filters typically decrease when the network goes deeper, and 3) these effective ranks are converging over training steps. Inspired by these observations, we propose a new layer called Separable Convolutional Eigen-Filters (SCEF) as an alternative parameterization to Conv2D filters. A SCEF layer can be easily implemented using the depthwise separable convolutions trained with our proposed training strategy. In addition to the decreased number of trainable parameters by using SCEF, depthwise separable convolutions are known to be more computationally efficient compared to Conv2D operations, which reduces the runtime FLOPs as well. Experiments are conducted on the CIFAR-10 and ImageNet datasets by replacing the Conv2D layers with SCEF. The results have shown an increased accuracy using about 2/3 of the original parameters and reduce the number of FLOPs to 2/3 of the base net.

Learning Hierarchical Feature Space Using CLAss-specific Subspace Multiple Kernel -- Metric Learning for Classification

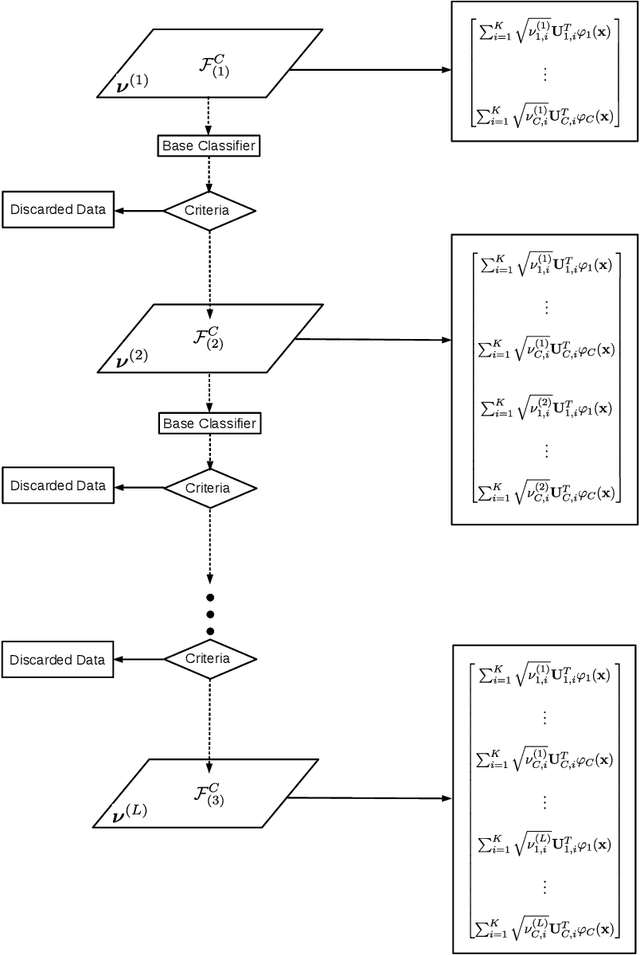
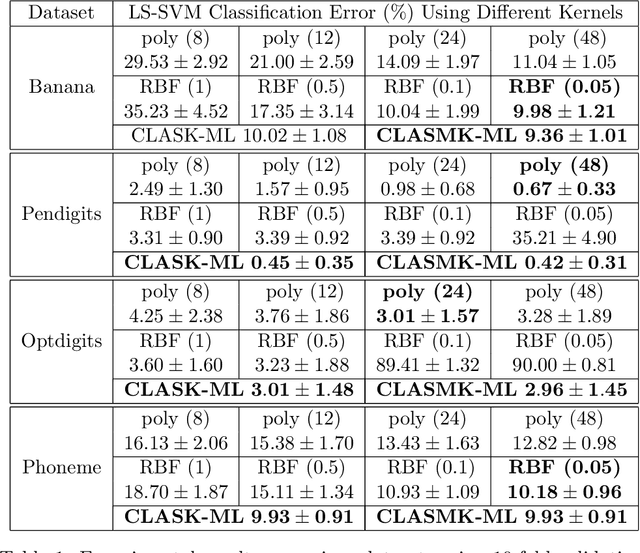
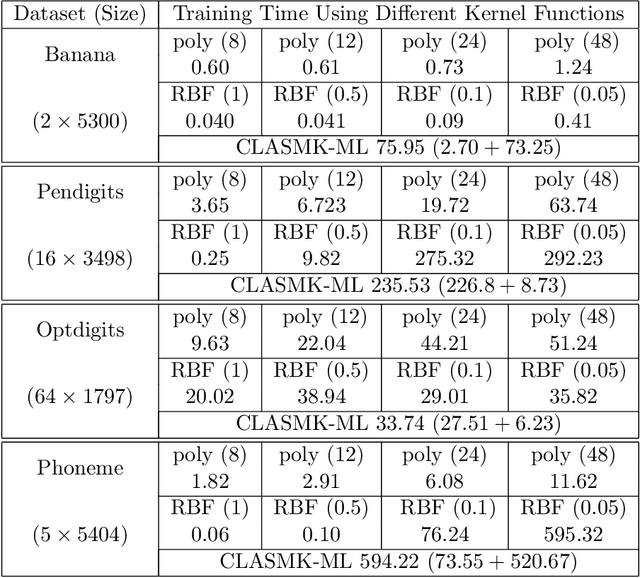
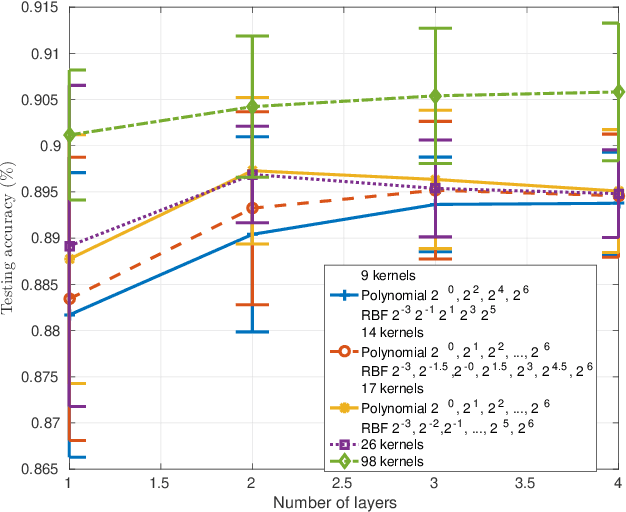
Metric learning for classification has been intensively studied over the last decade. The idea is to learn a metric space induced from a normed vector space on which data from different classes are well separated. Different measures of the separation thus lead to various designs of the objective function in the metric learning model. One classical metric is the Mahalanobis distance, where a linear transformation matrix is designed and applied on the original dataset to obtain a new subspace equipped with the Euclidean norm. The kernelized version has also been developed, followed by Multiple-Kernel learning models. In this paper, we consider metric learning to be the identification of the best kernel function with respect to a high class separability in the corresponding metric space. The contribution is twofold: 1) No pairwise computations are required as in most metric learning techniques; 2) Better flexibility and lower computational complexity is achieved using the CLAss-Specific (Multiple) Kernel - Metric Learning (CLAS(M)K-ML). The proposed techniques can be considered as a preprocessing step to any kernel method or kernel approximation technique. An extension to a hierarchical learning structure is also proposed to further improve the classification performance, where on each layer, the CLASMK is computed based on a selected "marginal" subset and feature vectors are constructed by concatenating the features from all previous layers.