Integrating Transformations in Probabilistic Circuits

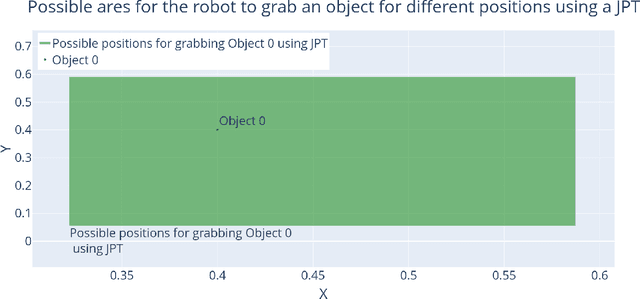
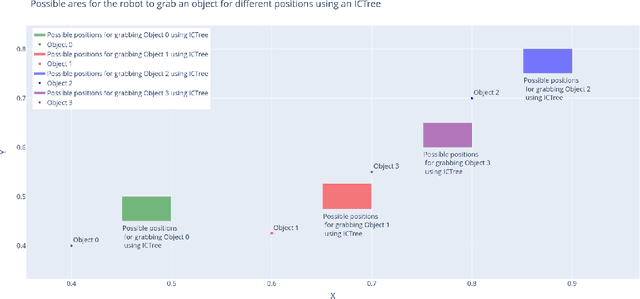
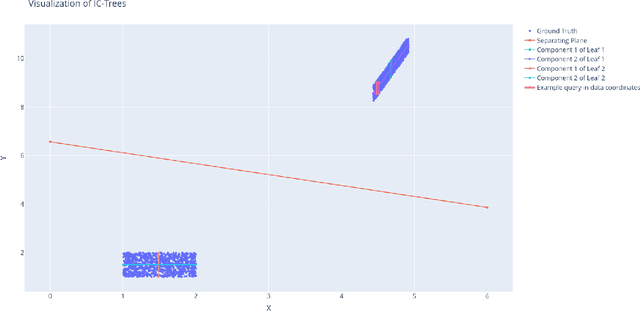
This study addresses the predictive limitation of probabilistic circuits and introduces transformations as a remedy to overcome it. We demonstrate this limitation in robotic scenarios. We motivate that independent component analysis is a sound tool to preserve the independence properties of probabilistic circuits. Our approach is an extension of joint probability trees, which are model-free deterministic circuits. By doing so, it is demonstrated that the proposed approach is able to achieve higher likelihoods while using fewer parameters compared to the joint probability trees on seven benchmark data sets as well as on real robot data. Furthermore, we discuss how to integrate transformations into tree-based learning routines. Finally, we argue that exact inference with transformed quantile parameterized distributions is not tractable. However, our approach allows for efficient sampling and approximate inference.

Joint Probability Trees

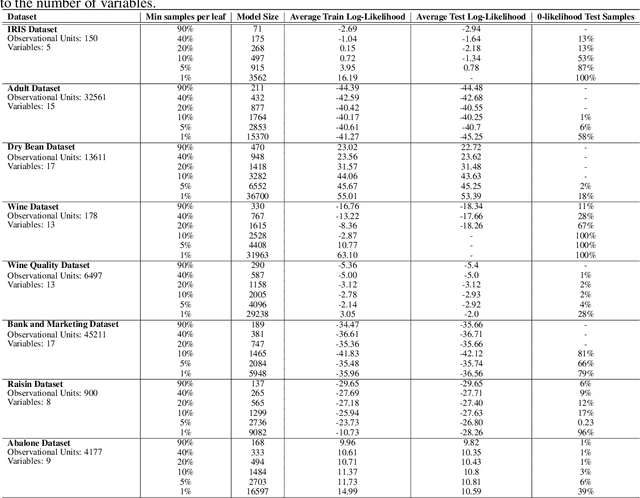
We introduce Joint Probability Trees (JPT), a novel approach that makes learning of and reasoning about joint probability distributions tractable for practical applications. JPTs support both symbolic and subsymbolic variables in a single hybrid model, and they do not rely on prior knowledge about variable dependencies or families of distributions. JPT representations build on tree structures that partition the problem space into relevant subregions that are elicited from the training data instead of postulating a rigid dependency model prior to learning. Learning and reasoning scale linearly in JPTs, and the tree structure allows white-box reasoning about any posterior probability $P(Q|E)$, such that interpretable explanations can be provided for any inference result. Our experiments showcase the practical applicability of JPTs in high-dimensional heterogeneous probability spaces with millions of training samples, making it a promising alternative to classic probabilistic graphical models.