Enhancing Score-Based Sampling Methods with Ensembles

We introduce ensembles within score-based sampling methods to develop gradient-free approximate sampling techniques that leverage the collective dynamics of particle ensembles to compute approximate reverse diffusion drifts. We introduce the underlying methodology, emphasizing its relationship with generative diffusion models and the previously introduced F\"ollmer sampler. We demonstrate the efficacy of ensemble strategies through various examples, ranging from low- to medium-dimensionality sampling problems, including multi-modal and highly non-Gaussian probability distributions, and provide comparisons to traditional methods like NUTS. Our findings highlight the potential of ensemble strategies for modeling complex probability distributions in situations where gradients are unavailable. Finally, we showcase its application in the context of Bayesian inversion problems within the geophysical sciences.

Easing Color Shifts in Score-Based Diffusion Models

Generated images of score-based models can suffer from errors in their spatial means, an effect, referred to as a color shift, which grows for larger images. This paper introduces a computationally inexpensive solution to mitigate color shifts in score-based diffusion models. We propose a simple nonlinear bypass connection in the score network, designed to process the spatial mean of the input and to predict the mean of the score function. This network architecture substantially improves the resulting spatial means of the generated images, and we show that the improvement is approximately independent of the size of the generated images. As a result, our solution offers a comparatively inexpensive solution for the color shift problem across image sizes. Lastly, we discuss the origin of color shifts in an idealized setting in order to motivate our approach.

Unpaired Downscaling of Fluid Flows with Diffusion Bridges

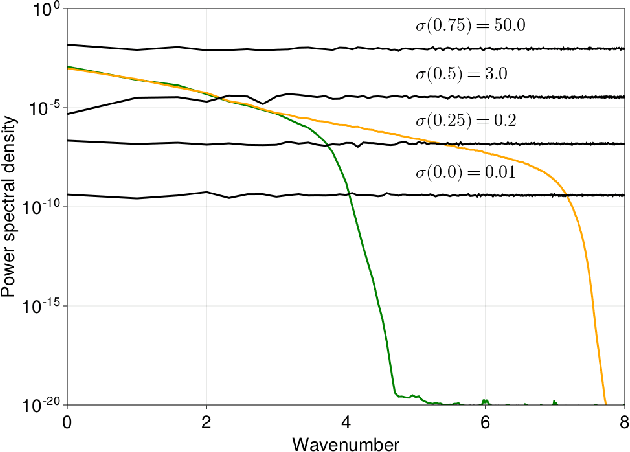
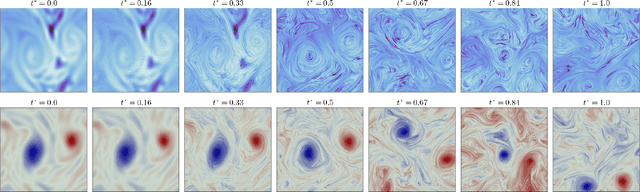
We present a method to downscale idealized geophysical fluid simulations using generative models based on diffusion maps. By analyzing the Fourier spectra of images drawn from different data distributions, we show how one can chain together two independent conditional diffusion models for use in domain translation. The resulting transformation is a diffusion bridge between a low resolution and a high resolution dataset and allows for new sample generation of high-resolution images given specific low resolution features. The ability to generate new samples allows for the computation of any statistic of interest, without any additional calibration or training. Our unsupervised setup is also designed to downscale images without access to paired training data; this flexibility allows for the combination of multiple source and target domains without additional training. We demonstrate that the method enhances resolution and corrects context-dependent biases in geophysical fluid simulations, including in extreme events. We anticipate that the same method can be used to downscale the output of climate simulations, including temperature and precipitation fields, without needing to train a new model for each application and providing a significant computational cost savings.

Unsupervised Discovery of El Nino Using Causal Feature Learning on Microlevel Climate Data

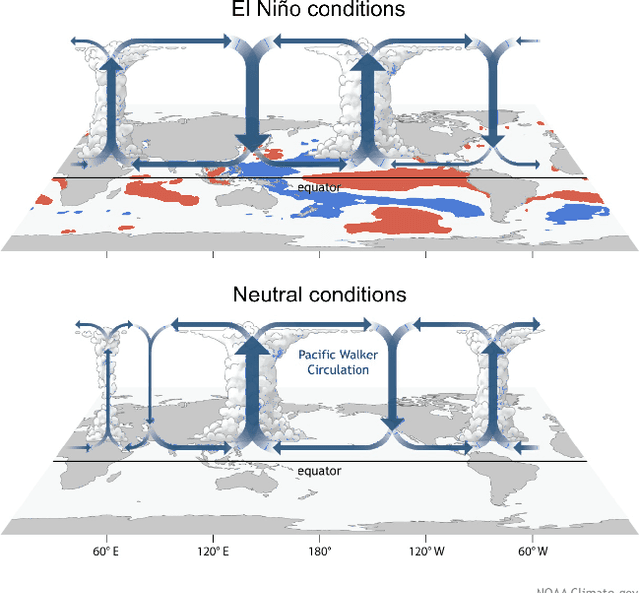
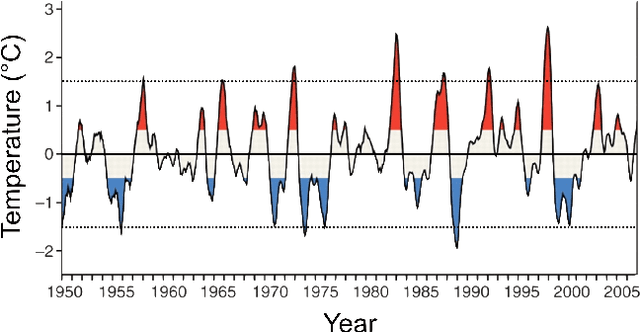
We show that the climate phenomena of El Nino and La Nina arise naturally as states of macro-variables when our recent causal feature learning framework (Chalupka 2015, Chalupka 2016) is applied to micro-level measures of zonal wind (ZW) and sea surface temperatures (SST) taken over the equatorial band of the Pacific Ocean. The method identifies these unusual climate states on the basis of the relation between ZW and SST patterns without any input about past occurrences of El Nino or La Nina. The simpler alternatives of (i) clustering the SST fields while disregarding their relationship with ZW patterns, or (ii) clustering the joint ZW-SST patterns, do not discover El Nino. We discuss the degree to which our method supports a causal interpretation and use a low-dimensional toy example to explain its success over other clustering approaches. Finally, we propose a new robust and scalable alternative to our original algorithm (Chalupka 2016), which circumvents the need for high-dimensional density learning.