A Translational Three-Degrees-of-Freedom Parallel Mechanism With Partial Motion Decoupling and Analytic Direct Kinematics

According to the topological design theory and method of parallel mechanism (PM) based on position and orientation characteristic (POC) equations, this paper studied a 3-DOF translational PM that has three advantages, i.e., (i) it consists of three fixed actuated prismatic joints, (ii) the PM has analytic solutions to the direct and inverse kinematic problems, and (iii) the PM is of partial motion decoupling property. Firstly, the main topological characteristics, such as the POC, degree of freedom and coupling degree were calculated for kinematic modeling. Thanks to these properties, the direct and inverse kinematic problems can be readily solved. Further, the conditions of the singular configurations of the PM were analyzed which corresponds to its partial motion decoupling property.

Topology design and analysis of a novel 3-translational parallel mechanism with analytical direct position solutions and partial motion decoupling

According to the topological design theory and method of parallel mechanism (PM) based on position and orientation characteristic (POC) equations, this paper design a novel 3-translation (3T) PM that has three advantages, i.e., 1) it consists on three actuated prismatic joints, 2) the PM has analytical direct position solutions, and 3) the PM is of partial motion decoupling property. Firstly, the main topological characteristics such as the POC, degree of freedom and coupling degree are calculated for kinematics modelling. Due to the special constraint feature of the 3-translation, the analytical direct position solutions of the PM can be directly obtained without needing to use one-dimensional search method. Further, the conditions of the singular configuration of the PM, as well as the singularity location inside the workspace are analyzed according to the inverse kinematics.

Topological design of an asymmetric 3-translational parallel mechanism with zero coupling degree and motion decoupling

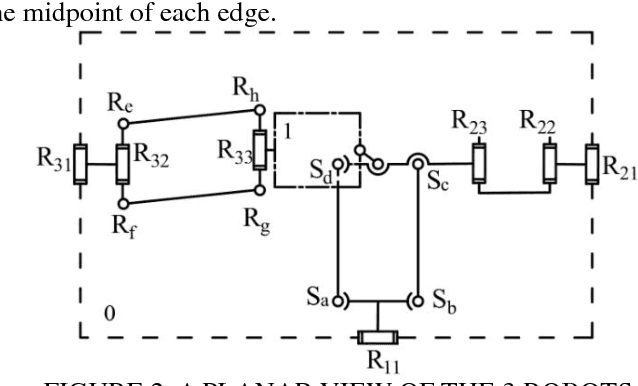
In this paper a new asymmetric 3-translational (3T) parallel manipulator, i.e., RPa(3R) 2R+RPa, with zero coupling degree and decoupled motion is firstly proposed according to topology design theory of parallel mechanism (PM) based on position and orientation characteristics (POC) equations. The main topological characteristics such as POC, degree of freedom and coupling degree are calculated. Then, the analytical formula for the direct and inverse kinematic are directly derived since coupling degree of the PM is zero. The study of singular configurations is simple because of the independence of the kinematic chains.