A new 3-DOF 2T1R parallel mechanism: Topology design and kinematics

This article presents a new three-degree-of-freedom (3-DOF) parallel mechanism (PM) with two translations and one rotation (2T1R), designed based on the topological design theory of the parallel mechanism using position and orientation characteristics (POC). The PM is primarily intended for use in package sorting and delivery. The mobile platform of the PM moves along a translation axis, picks up objects from a conveyor belt, and tilts them to either side of the axis. We first calculate the PM's topological characteristics, such as the degree of freedom (DOF) and the degree of coupling, and provide its topological analytical formula to represent the topological information of the PM. Next, we solve the direct and inverse kinematic models based on the kinematic modelling principle using the topological features. The models are purely analytic and are broken down into a series of quadratic equations, making them suitable for use in an industrial robot. We also study the singular configurations to identify the serial and parallel singularities. Using the decoupling properties, we size the mechanism to address the package sorting and depositing problem using an algebraic approach. To determine the smallest segment lengths, we use a cylindrical algebraic decomposition to solve a system with inequalities.

A novel partially-decoupled translational parallel manipulator with symbolic kinematics, singularity identification and workspace determination

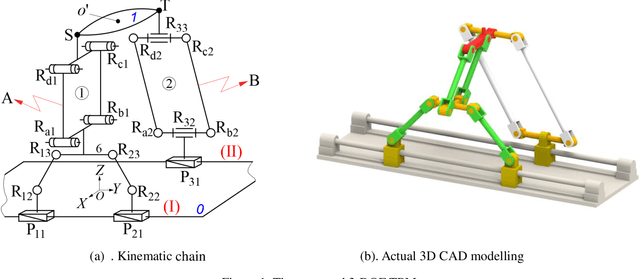
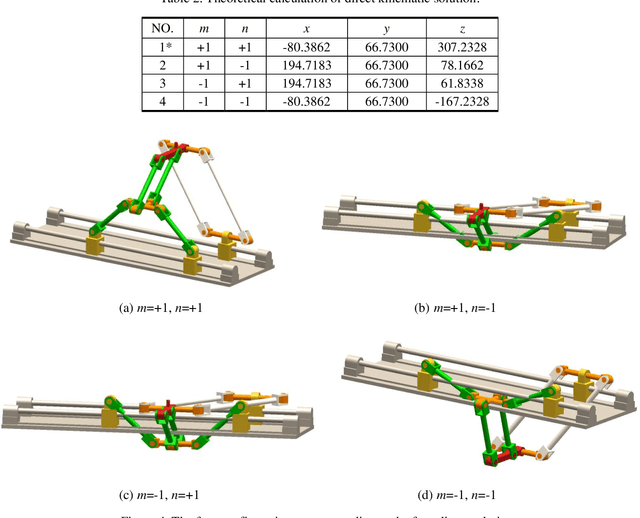
This paper presents a novel three-degree-of-freedom (3-DOF) translational parallel manipulator (TPM) by using a topological design method of parallel mechanism (PM) based on position and orientation characteristic (POC) equations. The proposed PM is only composed of lower-mobility joints and actuated prismatic joints, together with the investigations on three kinematic issues of importance. The first aspect pertains to geometric modeling of the TPM in connection with its topological characteristics, such as the POC, degree of freedom and coupling degree, from which its symbolic direct kinematic solutions are readily obtained. Moreover, the decoupled properties of input-output motions are directly evaluated without Jacobian analysis. Sequentially, based upon the inverse kinematics, the singular configurations of the TPM are identified, wherein the singular surfaces are visualized by means of a Gr{\"o}bner based elimination operation. Finally, the workspace of the TPM is evaluated with a geometric approach. This 3-DOF TPM features less joints and links compared with the well-known Delta robot, which reduces the structural complexity. Its symbolic direct kinematics and partially-decoupled property will ease path planning and dynamic analysis. The TPM can be used for manufacturing large work pieces.

A Translational Three-Degrees-of-Freedom Parallel Mechanism With Partial Motion Decoupling and Analytic Direct Kinematics

According to the topological design theory and method of parallel mechanism (PM) based on position and orientation characteristic (POC) equations, this paper studied a 3-DOF translational PM that has three advantages, i.e., (i) it consists of three fixed actuated prismatic joints, (ii) the PM has analytic solutions to the direct and inverse kinematic problems, and (iii) the PM is of partial motion decoupling property. Firstly, the main topological characteristics, such as the POC, degree of freedom and coupling degree were calculated for kinematic modeling. Thanks to these properties, the direct and inverse kinematic problems can be readily solved. Further, the conditions of the singular configurations of the PM were analyzed which corresponds to its partial motion decoupling property.

Topology design and analysis of a novel 3-translational parallel mechanism with analytical direct position solutions and partial motion decoupling

According to the topological design theory and method of parallel mechanism (PM) based on position and orientation characteristic (POC) equations, this paper design a novel 3-translation (3T) PM that has three advantages, i.e., 1) it consists on three actuated prismatic joints, 2) the PM has analytical direct position solutions, and 3) the PM is of partial motion decoupling property. Firstly, the main topological characteristics such as the POC, degree of freedom and coupling degree are calculated for kinematics modelling. Due to the special constraint feature of the 3-translation, the analytical direct position solutions of the PM can be directly obtained without needing to use one-dimensional search method. Further, the conditions of the singular configuration of the PM, as well as the singularity location inside the workspace are analyzed according to the inverse kinematics.

Automatic mobility analysis of parallel mechanisms: an algorithm approach based on position and orientation characteristic equations

The determination of the mobility of parallel mechanisms (PM) is a fundamental problem. An automatic and intelligent analysis platform will be a significant tool for the design and optimization of mechanical systems. Based on the theory of position and orientation characteristics (POC) equations, a systematic approach to computer-aided mobility analysis of PMs is presented in this paper. First, a digital model for topological structures which has a mapping relationship with position and orientation characteristics of mechanism is proposed. It describes not only the dimension of the motion output, but also gives the mapping relationship between the output characteristic and the axis of the kinematic joints. Secondly, algorithmic rules are established that convert the union and intersection operations of POC into the binary logical operations and the automatic analysis of POC are realized. Then, the algorithm of the automatic mobility analysis of PMs and its implementation with VC++ are written .The mobility and its properties (POC) will also be analyzed and displayed automatically after introducing by users of the data of topological structures representation. Finally, typical examples are provided to show the effectiveness of the software platform.

Topological design of an asymmetric 3-translational parallel mechanism with zero coupling degree and motion decoupling

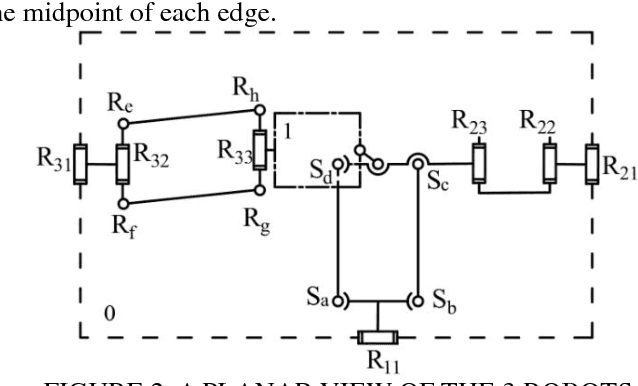
In this paper a new asymmetric 3-translational (3T) parallel manipulator, i.e., RPa(3R) 2R+RPa, with zero coupling degree and decoupled motion is firstly proposed according to topology design theory of parallel mechanism (PM) based on position and orientation characteristics (POC) equations. The main topological characteristics such as POC, degree of freedom and coupling degree are calculated. Then, the analytical formula for the direct and inverse kinematic are directly derived since coupling degree of the PM is zero. The study of singular configurations is simple because of the independence of the kinematic chains.