Deep Learning of Potential Outcomes

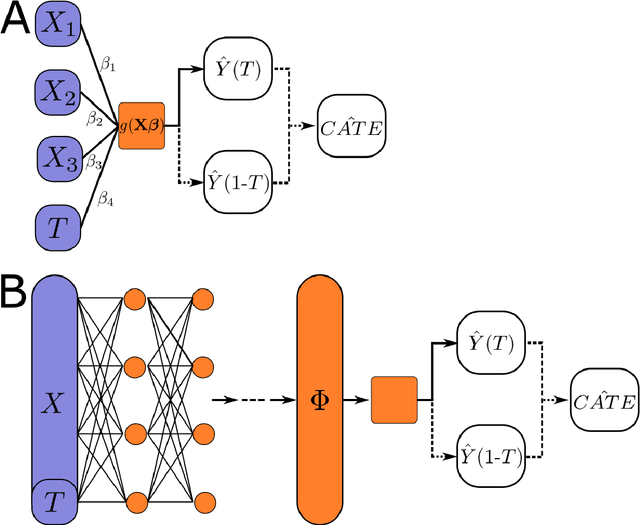
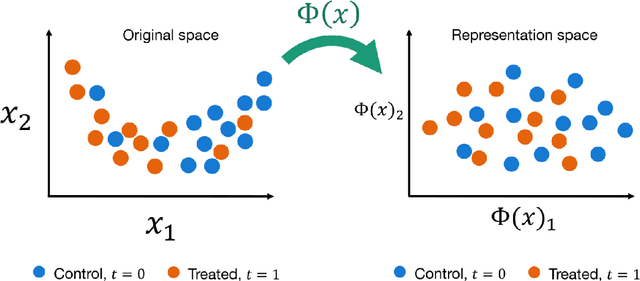
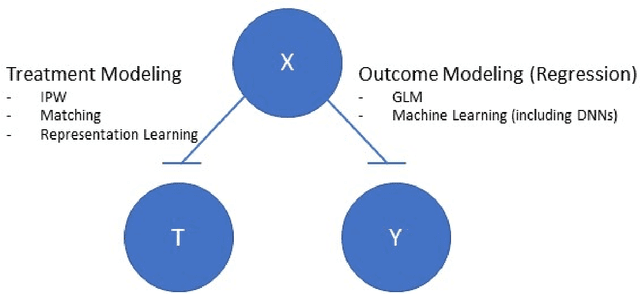
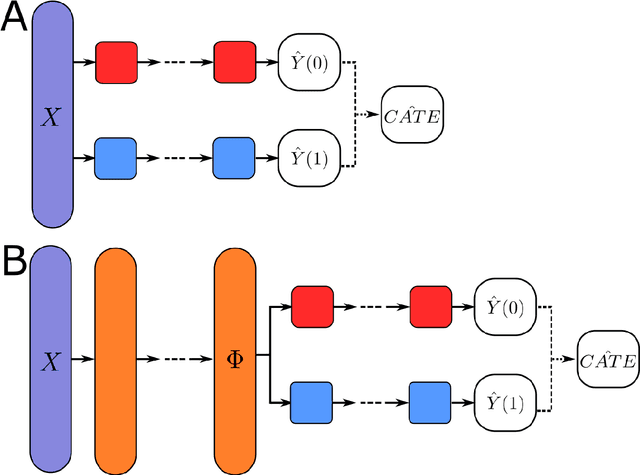
This review systematizes the emerging literature for causal inference using deep neural networks under the potential outcomes framework. It provides an intuitive introduction on how deep learning can be used to estimate/predict heterogeneous treatment effects and extend causal inference to settings where confounding is non-linear, time varying, or encoded in text, networks, and images. To maximize accessibility, we also introduce prerequisite concepts from causal inference and deep learning. The survey differs from other treatments of deep learning and causal inference in its sharp focus on observational causal estimation, its extended exposition of key algorithms, and its detailed tutorials for implementing, training, and selecting among deep estimators in Tensorflow 2 available at github.com/kochbj/Deep-Learning-for-Causal-Inference.

Parametric UMAP: learning embeddings with deep neural networks for representation and semi-supervised learning

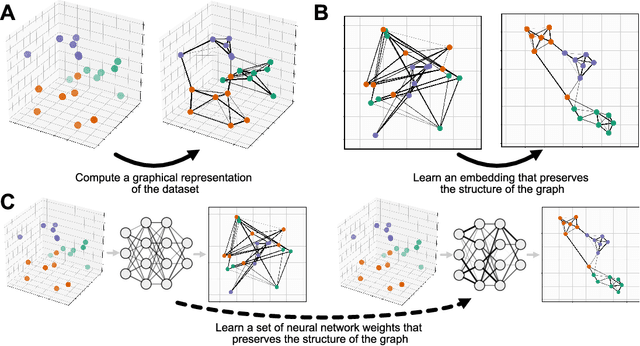
We propose Parametric UMAP, a parametric variation of the UMAP (Uniform Manifold Approximation and Projection) algorithm. UMAP is a non-parametric graph-based dimensionality reduction algorithm using applied Riemannian geometry and algebraic topology to find low-dimensional embeddings of structured data. The UMAP algorithm consists of two steps: (1) Compute a graphical representation of a dataset (fuzzy simplicial complex), and (2) Through stochastic gradient descent, optimize a low-dimensional embedding of the graph. Here, we replace the second step of UMAP with a deep neural network that learns a parametric relationship between data and embedding. We demonstrate that our method performs similarly to its non-parametric counterpart while conferring the benefit of a learned parametric mapping (e.g. fast online embeddings for new data). We then show that UMAP loss can be extended to arbitrary deep learning applications, for example constraining the latent distribution of autoencoders, and improving classifier accuracy for semi-supervised learning by capturing structure in unlabeled data. Our code is available at https://github.com/timsainb/ParametricUMAP_paper.

Generative adversarial interpolative autoencoding: adversarial training on latent space interpolations encourage convex latent distributions

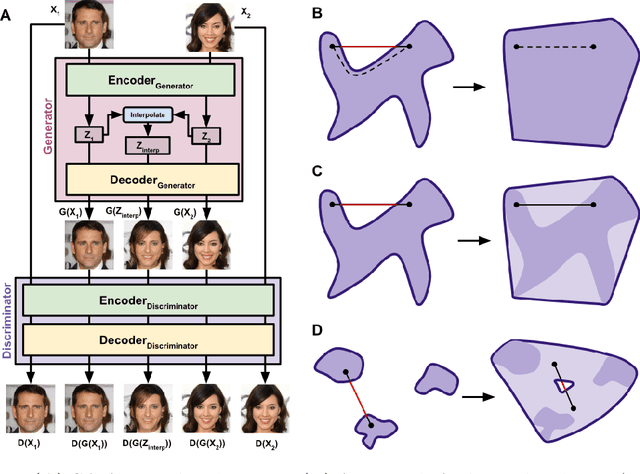
We present a neural network architecture based upon the Autoencoder (AE) and Generative Adversarial Network (GAN) that promotes a convex latent distribution by training adversarially on latent space interpolations. By using an AE as both the generator and discriminator of a GAN, we pass a pixel-wise error function across the discriminator, yielding an AE which produces non-blurry samples that match both high- and low-level features of the original images. Interpolations between images in this space remain within the latent-space distribution of real images as trained by the discriminator, and therfore preserve realistic resemblances to the network inputs.