Improving Mapper's Robustness by Varying Resolution According to Lens-Space Density

We propose an improvement to the Mapper algorithm that removes the assumption of a single resolution scale across semantic space, and improves the robustness of the results under change of parameters. This eases parameter selection, especially for datasets with highly variable local density in the Morse function $f$ used for Mapper. This is achieved by incorporating this density into the choice of cover for Mapper. Furthermore, we prove that for covers with some natural hypotheses, the graph output by Mapper still converges in bottleneck distance to the Reeb graph of the Rips complex of the data, but captures more topological features than when using the usual Mapper cover. Finally, we discuss implementation details, and include the results of computational experiments. We also provide an accompanying reference implementation.

Parametric UMAP: learning embeddings with deep neural networks for representation and semi-supervised learning

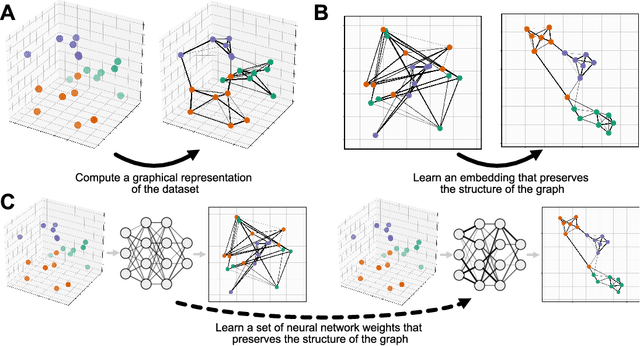
We propose Parametric UMAP, a parametric variation of the UMAP (Uniform Manifold Approximation and Projection) algorithm. UMAP is a non-parametric graph-based dimensionality reduction algorithm using applied Riemannian geometry and algebraic topology to find low-dimensional embeddings of structured data. The UMAP algorithm consists of two steps: (1) Compute a graphical representation of a dataset (fuzzy simplicial complex), and (2) Through stochastic gradient descent, optimize a low-dimensional embedding of the graph. Here, we replace the second step of UMAP with a deep neural network that learns a parametric relationship between data and embedding. We demonstrate that our method performs similarly to its non-parametric counterpart while conferring the benefit of a learned parametric mapping (e.g. fast online embeddings for new data). We then show that UMAP loss can be extended to arbitrary deep learning applications, for example constraining the latent distribution of autoencoders, and improving classifier accuracy for semi-supervised learning by capturing structure in unlabeled data. Our code is available at https://github.com/timsainb/ParametricUMAP_paper.

Manifold Learning of Four-dimensional Scanning Transmission Electron Microscopy

Four-dimensional scanning transmission electron microscopy (4D-STEM) of local atomic diffraction patterns is emerging as a powerful technique for probing intricate details of atomic structure and atomic electric fields. However, efficient processing and interpretation of large volumes of data remain challenging, especially for two-dimensional or light materials because the diffraction signal recorded on the pixelated arrays is weak. Here we employ data-driven manifold leaning approaches for straightforward visualization and exploration analysis of the 4D-STEM datasets, distilling real-space neighboring effects on atomically resolved deflection patterns from single-layer graphene, with single dopant atoms, as recorded on a pixelated detector. These extracted patterns relate to both individual atom sites and sublattice structures, effectively discriminating single dopant anomalies via multi-mode views. We believe manifold learning analysis will accelerate physics discoveries coupled between data-rich imaging mechanisms and materials such as ferroelectric, topological spin and van der Waals heterostructures.

UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction

UMAP (Uniform Manifold Approximation and Projection) is a novel manifold learning technique for dimension reduction. UMAP is constructed from a theoretical framework based in Riemannian geometry and algebraic topology. The result is a practical scalable algorithm that applies to real world data. The UMAP algorithm is competitive with t-SNE for visualization quality, and arguably preserves more of the global structure with superior run time performance. Furthermore, UMAP as described has no computational restrictions on embedding dimension, making it viable as a general purpose dimension reduction technique for machine learning.

Accelerated Hierarchical Density Clustering

We present an accelerated algorithm for hierarchical density based clustering. Our new algorithm improves upon HDBSCAN*, which itself provided a significant qualitative improvement over the popular DBSCAN algorithm. The accelerated HDBSCAN* algorithm provides comparable performance to DBSCAN, while supporting variable density clusters, and eliminating the need for the difficult to tune distance scale parameter. This makes accelerated HDBSCAN* the default choice for density based clustering. Library available at: https://github.com/scikit-learn-contrib/hdbscan