Tianju Xu
Scaling Distributed Training with Adaptive Summation
Jun 04, 2020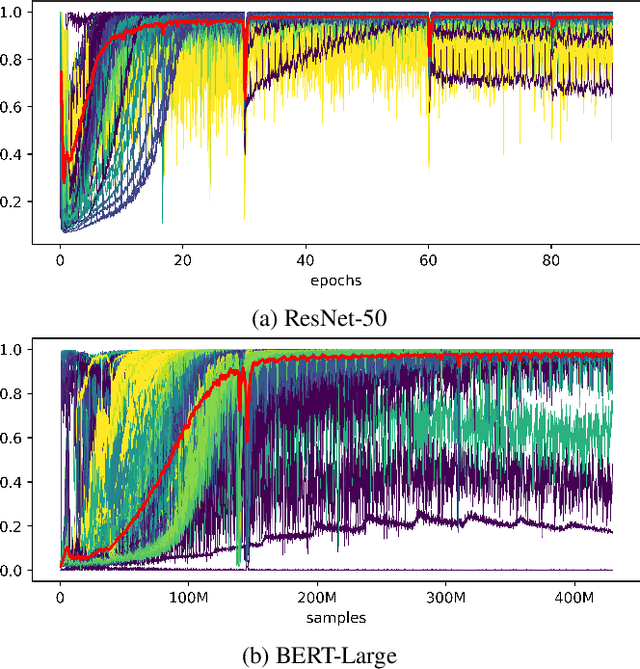
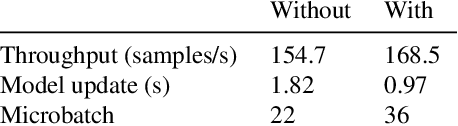
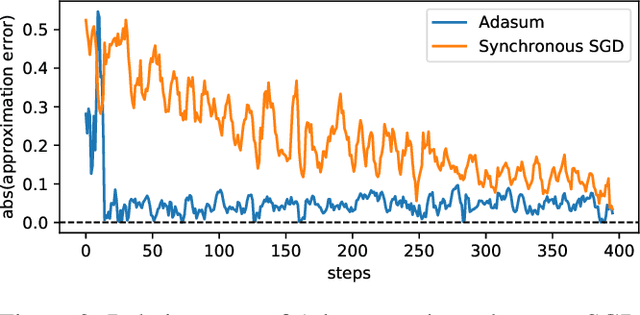

Abstract:Stochastic gradient descent (SGD) is an inherently sequential training algorithm--computing the gradient at batch $i$ depends on the model parameters learned from batch $i-1$. Prior approaches that break this dependence do not honor them (e.g., sum the gradients for each batch, which is not what sequential SGD would do) and thus potentially suffer from poor convergence. This paper introduces a novel method to combine gradients called Adasum (for adaptive sum) that converges faster than prior work. Adasum is easy to implement, almost as efficient as simply summing gradients, and is integrated into the open-source toolkit Horovod. This paper first provides a formal justification for Adasum and then empirically demonstrates Adasum is more accurate than prior gradient accumulation methods. It then introduces a series of case-studies to show Adasum works with multiple frameworks, (TensorFlow and PyTorch), scales multiple optimizers (Momentum-SGD, Adam, and LAMB) to larger batch-sizes while still giving good downstream accuracy. Finally, it proves that Adasum converges. To summarize, Adasum scales Momentum-SGD on the MLPerf Resnet50 benchmark to 64K examples before communication (no MLPerf v0.5 entry converged with more than 16K), the Adam optimizer to 64K examples before communication on BERT-LARGE (prior work showed Adam stopped scaling at 16K), and the LAMB optimizer to 128K before communication on BERT-LARGE (prior work used 64K), all while maintaining downstream accuracy metrics. Finally, if a user does not need to scale, we show LAMB with Adasum on BERT-LARGE converges in 30% fewer steps than the baseline.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge