Tianhui Zhou
Multiple Domain Causal Networks
May 13, 2022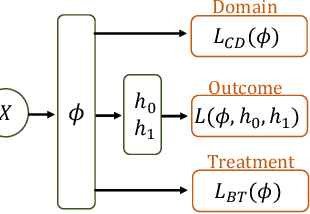


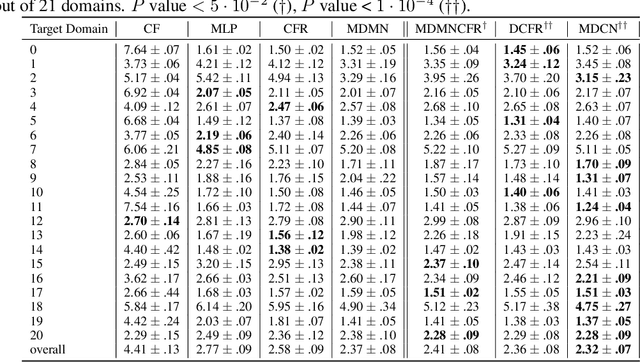
Abstract:Observational studies are regarded as economic alternatives to randomized trials, often used in their stead to investigate and determine treatment efficacy. Due to lack of sample size, observational studies commonly combine data from multiple sources or different sites/centers. Despite the benefits of an increased sample size, a naive combination of multicenter data may result in incongruities stemming from center-specific protocols for generating cohorts or reactions towards treatments distinct to a given center, among other things. These issues arise in a variety of other contexts, including capturing a treatment effect related to an individual's unique biological characteristics. Existing methods for estimating heterogeneous treatment effects have not adequately addressed the multicenter context, but rather treat it simply as a means to obtain sufficient sample size. Additionally, previous approaches to estimating treatment effects do not straightforwardly generalize to the multicenter design, especially when required to provide treatment insights for patients from a new, unobserved center. To address these shortcomings, we propose Multiple Domain Causal Networks (MDCN), an approach that simultaneously strengthens the information sharing between similar centers while addressing the selection bias in treatment assignment through learning of a new feature embedding. In empirical evaluations, MDCN is consistently more accurate when estimating the heterogeneous treatment effect in new centers compared to benchmarks that adjust solely based on treatment imbalance or general center differences. Finally, we justify our approach by providing theoretical analyses that demonstrate that MDCN improves on the generalization bound of the new, unobserved target center.
Estimating Potential Outcome Distributions with Collaborating Causal Networks
Oct 04, 2021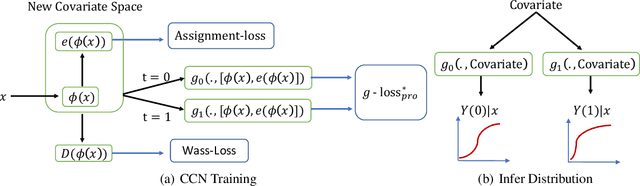

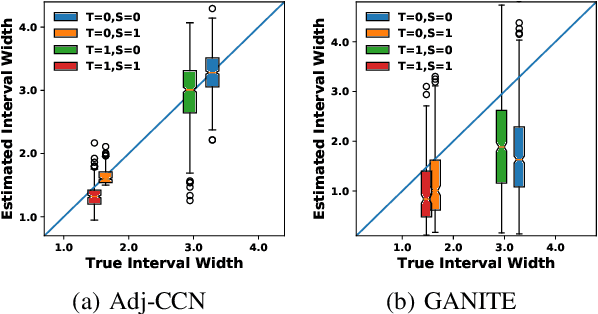
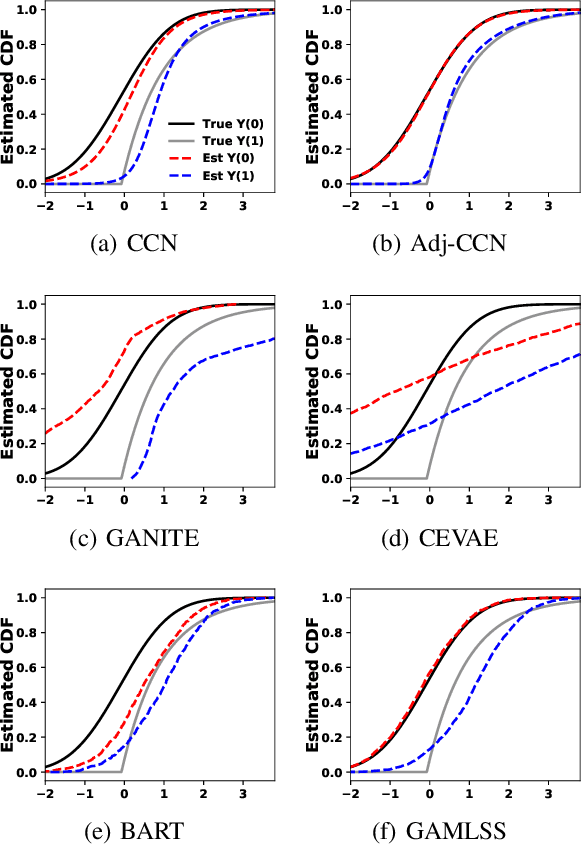
Abstract:Many causal inference approaches have focused on identifying an individual's outcome change due to a potential treatment, or the individual treatment effect (ITE), from observational studies. Rather than only estimating the ITE, we propose Collaborating Causal Networks (CCN) to estimate the full potential outcome distributions. This modification facilitates estimating the utility of each treatment and allows for individual variation in utility functions (e.g., variability in risk tolerance). We show that CCN learns distributions that asymptotically capture the correct potential outcome distributions under standard causal inference assumptions. Furthermore, we develop a new adjustment approach that is empirically effective in alleviating sample imbalance between treatment groups in observational studies. We evaluate CCN by extensive empirical experiments and demonstrate improved distribution estimates compared to existing Bayesian and Generative Adversarial Network-based methods. Additionally, CCN empirically improves decisions over a variety of utility functions.
Estimating Uncertainty Intervals from Collaborating Networks
Feb 12, 2020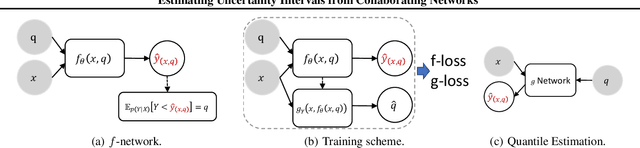

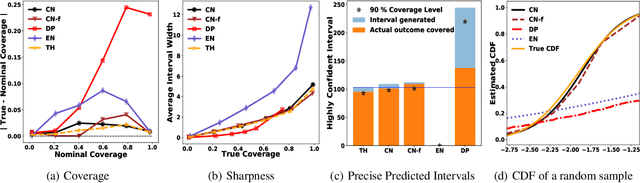

Abstract:Effective decision making requires understanding the uncertainty inherent in a prediction. To estimate uncertainty in regression, one could modify a deep neural network to predict coverage intervals, such as by predicting the mean and standard deviation. Unfortunately, in our empirical evaluations the predicted coverage from existing approaches is either overconfident or lacks sharpness (gives imprecise intervals). To address this challenge, we propose a novel method to estimate uncertainty based on two distinct neural networks with two distinct loss functions in a similar vein to Generative Adversarial Networks. Specifically, one network tries to learn the cumulative distribution function, and the second network tries to learn its inverse. Theoretical analysis demonstrates that the idealized solution is a fixed point and that under certain conditions the approach is asymptotically consistent to ground truth. We benchmark the approach on one synthetic and five real-world datasets, including forecasting A1c values in diabetic patients from electronic health records, where uncertainty is critical. In synthetic data, the proposed approach essentially matches the theoretically optimal solution in all aspects. In the real datasets, the proposed approach is empirically more faithful in its coverage estimates and typically gives sharper intervals than competing methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge