Estimating Uncertainty Intervals from Collaborating Networks

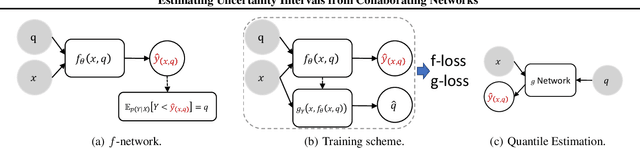
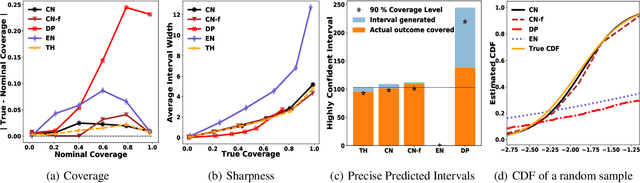
Effective decision making requires understanding the uncertainty inherent in a prediction. To estimate uncertainty in regression, one could modify a deep neural network to predict coverage intervals, such as by predicting the mean and standard deviation. Unfortunately, in our empirical evaluations the predicted coverage from existing approaches is either overconfident or lacks sharpness (gives imprecise intervals). To address this challenge, we propose a novel method to estimate uncertainty based on two distinct neural networks with two distinct loss functions in a similar vein to Generative Adversarial Networks. Specifically, one network tries to learn the cumulative distribution function, and the second network tries to learn its inverse. Theoretical analysis demonstrates that the idealized solution is a fixed point and that under certain conditions the approach is asymptotically consistent to ground truth. We benchmark the approach on one synthetic and five real-world datasets, including forecasting A1c values in diabetic patients from electronic health records, where uncertainty is critical. In synthetic data, the proposed approach essentially matches the theoretically optimal solution in all aspects. In the real datasets, the proposed approach is empirically more faithful in its coverage estimates and typically gives sharper intervals than competing methods.