Multiobject Tracking for Thresholded Cell Measurements

In many multiobject tracking applications, including radar and sonar tracking, after prefiltering the received signal, measurement data is typically structured in cells. The cells, e.g., represent different range and bearing values. However, conventional multiobject tracking methods use so-called point measurements. Point measurements are provided by a preprocessing stage that applies a threshold or detector and breaks up the cell's structure by converting cell indexes into, e.g., range and bearing measurements. We here propose a Bayesian multiobject tracking method that processes measurements that have been thresholded but are still cell-structured. We first derive a likelihood function that systematically incorporates an adjustable detection threshold which makes it possible to control the number of cell measurements. We then propose a Poisson Multi-Bernoulli (PMB) filter based on the likelihood function for cell measurements. Furthermore, we establish a link to the conventional point measurement model by deriving the likelihood function for point measurements with amplitude information (AM) and discuss the PMB filter that uses point measurements with AM. Our numerical results demonstrate the advantages of the proposed method that relies on thresholded cell measurements compared to the conventional multiobject tracking based on point measurements with and without AM.

To Coalesce or to Repel? An Analysis of MHT, JPDA, and Belief Propagation Multitarget Tracking Methods

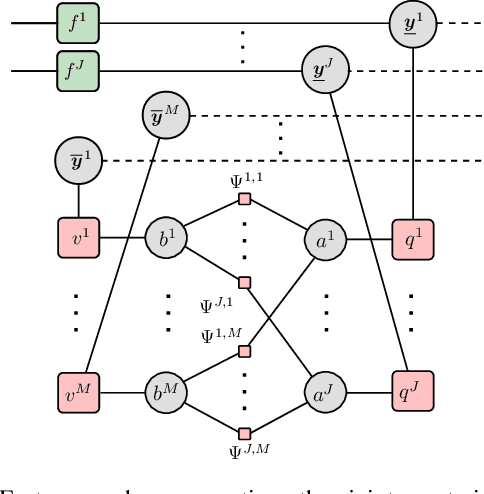
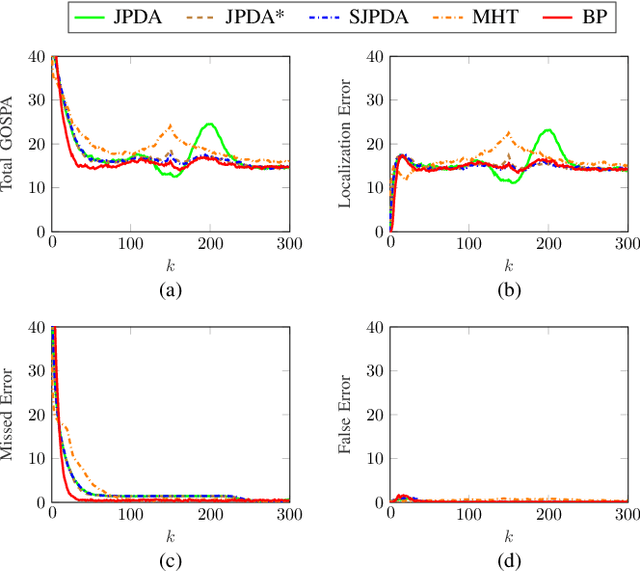
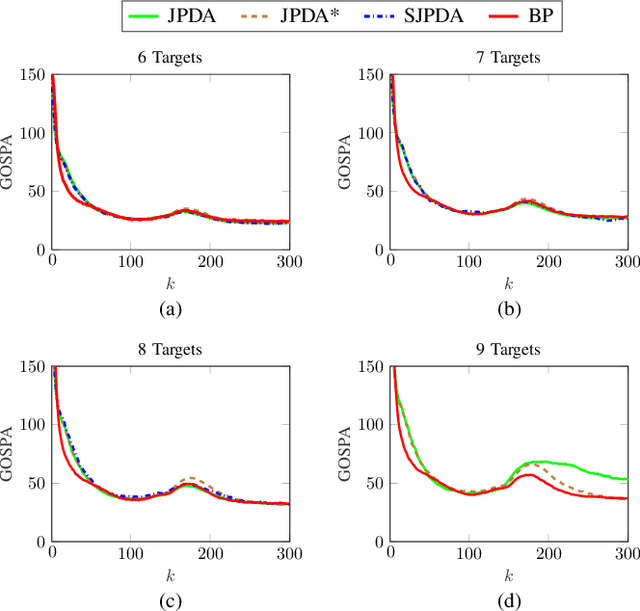
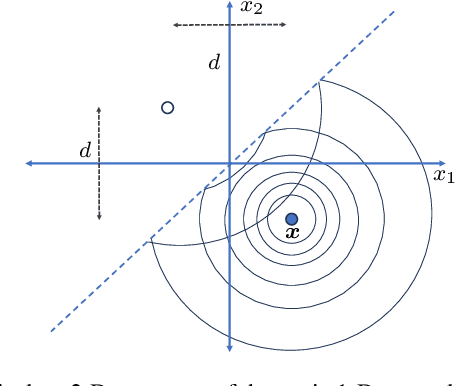
Joint probabilistic data association (JPDA) filter methods and multiple hypothesis tracking (MHT) methods are widely used for multitarget tracking (MTT). However, they are known to exhibit undesirable behavior in tracking scenarios with targets in close proximity: JPDA filter methods suffer from the track coalescence effect, i.e., the estimated tracks of targets in close proximity tend to merge and can become indistinguishable, and MHT methods suffer from an opposite effect known as track repulsion. In this paper, we review the JPDA filter and MHT methods and discuss the track coalescence and track repulsion effects. We also consider a more recent methodology for MTT that is based on the belief propagation (BP) algorithm, and we argue that BP-based MTT exhibits significantly reduced track coalescence and no track repulsion. Our theoretical arguments are confirmed by numerical results.

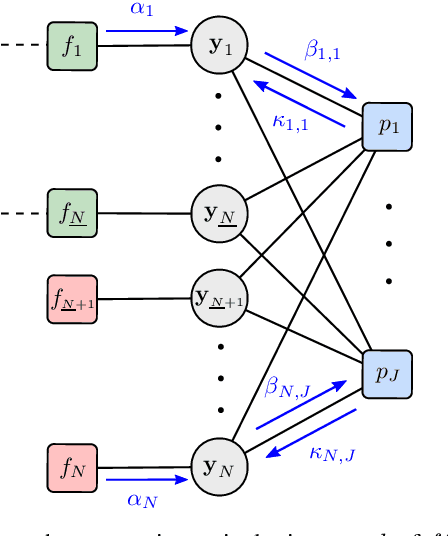
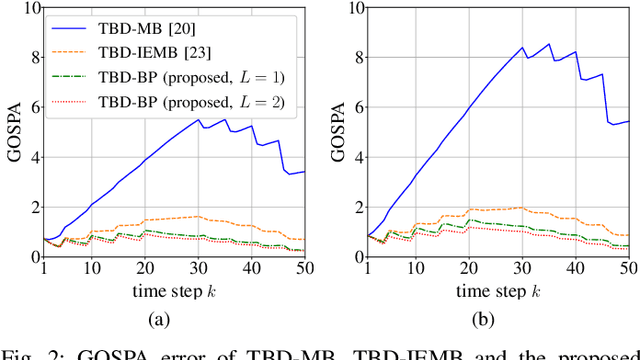
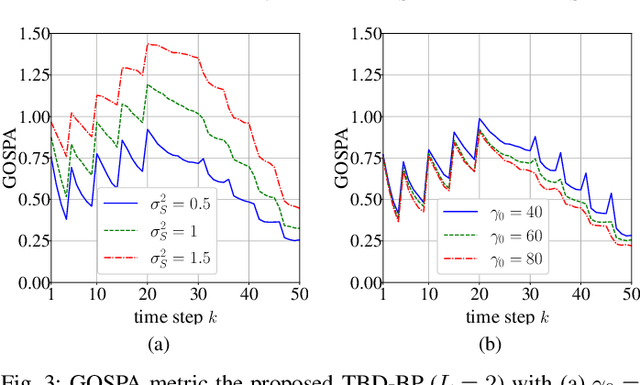
A BP Method for Track-Before-Detect

Tracking an unknown number of low-observable objects is notoriously challenging. This letter proposes a sequential Bayesian estimation method based on the track-before-detect (TBD) approach. In TBD, raw sensor measurements are directly used by the tracking algorithm without any preprocessing. Our proposed method is based on a new statistical model that introduces a new object hypothesis for each data cell of the raw sensor measurements. It allows objects to interact and contribute to more than one data cell. Based on the factor graph representing our statistical model, we derive the message passing equations of the proposed belief propagation (BP) method for TBD. Approximations are applied to certain BP messages to reduce computational complexity and improve scalability. In a simulation experiment, our proposed BP-based TBD method outperforms two other state-of-the-art TBD methods.

An Efficient Labeled/Unlabeled Random Finite Set Algorithm for Multiobject Tracking

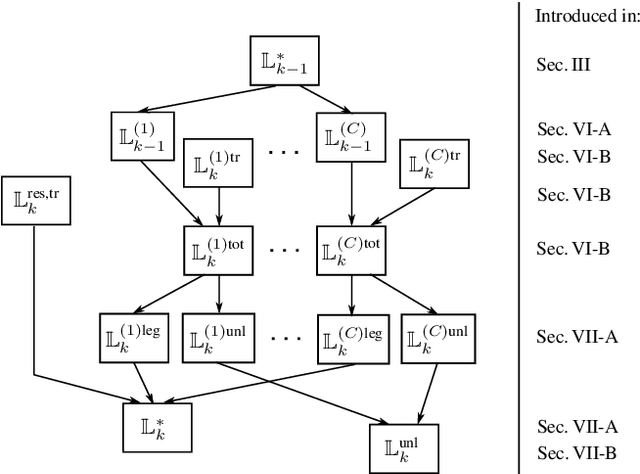
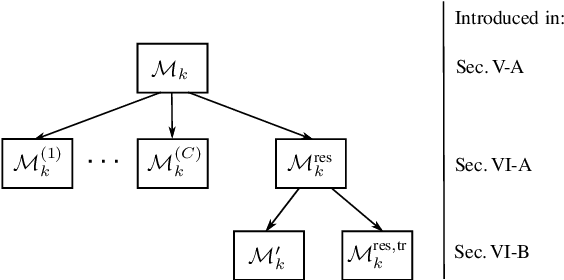
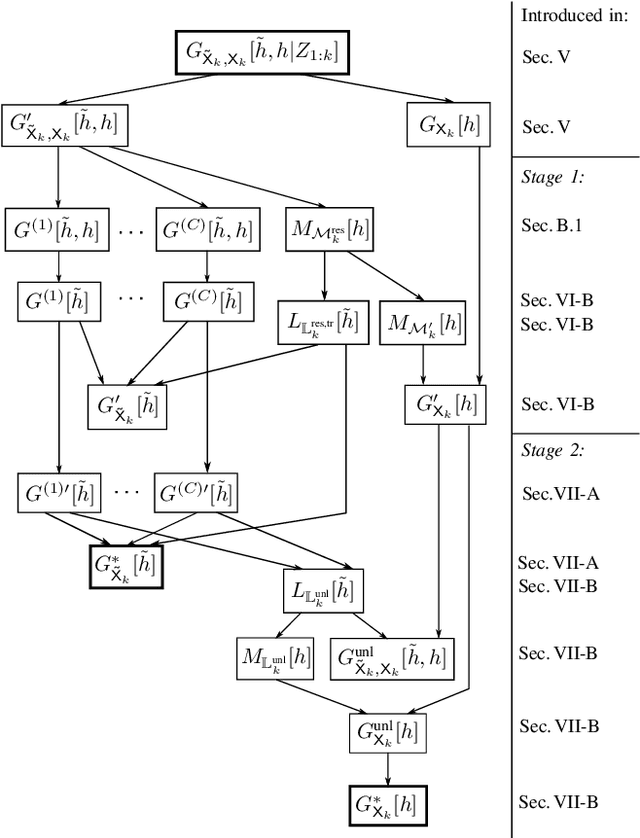
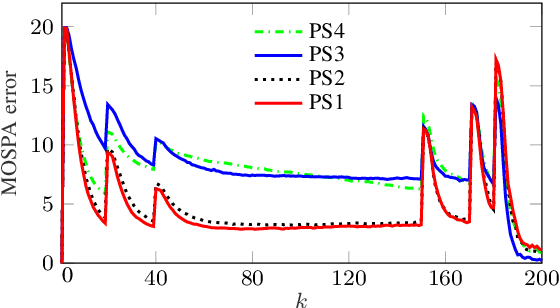
We propose an efficient random finite set (RFS) based algorithm for multiobject tracking in which the object states are modeled by a combination of a labeled multi-Bernoulli (LMB) RFS and a Poisson RFS. The less computationally demanding Poisson part of the algorithm is used to track potential objects whose existence is unlikely. Only if a quantity characterizing the plausibility of object existence is above a threshold, a new LMB component is created and the object is tracked by the more accurate but more computationally demanding LMB part of the algorithm. Conversely, an LMB component is transferred back to the Poisson RFS if the corresponding existence probability falls below a threshold. Contrary to existing hybrid algorithms based on multi-Bernoulli and Poisson RFSs, the proposed method facilitates track continuity and implements complexity-reducing features. Simulation results demonstrate a large complexity reduction relative to other RFS-based algorithms with comparable performance.

Track Coalescence and Repulsion: MHT, JPDA, and BP

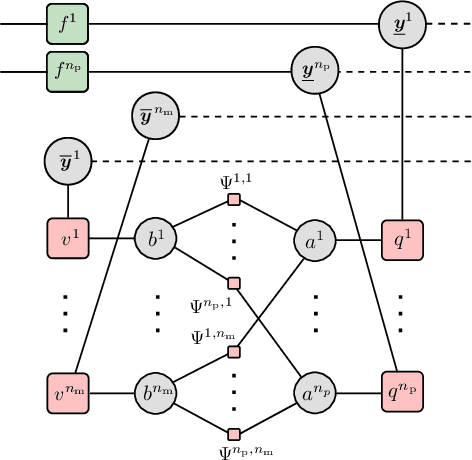
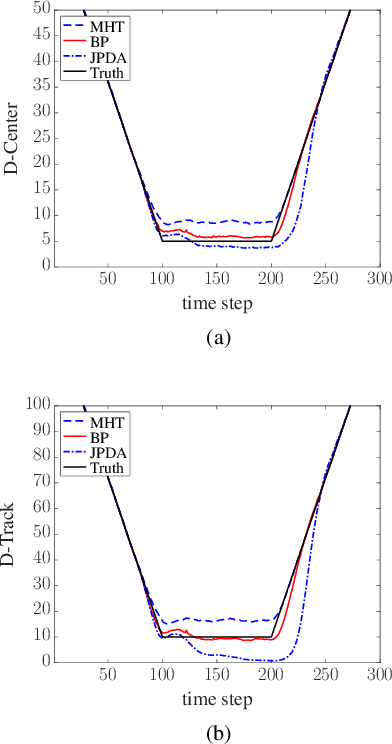
Joint probabilistic data association (JPDA) and multiple hypothesis tracking (MHT) introduced in the 70s, are still widely used methods for multitarget tracking (MTT). Extensive studies over the last few decades have revealed undesirable behavior of JPDA and MHT type methods in tracking scenarios with targets in close proximity. In particular, JPDA suffers from the track coalescence effect, i.e., estimated tracks of targets in close proximity tend to merge and can become indistinguishable. Interestingly, in MHT, an opposite effect to track coalescence called track repulsion can be observed. In this paper, we review the estimation strategies of the MHT, JPDA, and the recently introduced belief propagation (BP) framework for MTT and we investigate if BP also suffers from these two detrimental effects. Our numerical results indicate that BP-based MTT can mostly avoid both track repulsion and coalescence.

A Scalable Track-Before-Detect Method With Poisson/Multi-Bernoulli Model

We propose a scalable track-before-detect (TBD) tracking method based on a Poisson/multi-Bernoulli model. To limit computational complexity, we approximate the exact multi-Bernoulli mixture posterior probability density function (pdf) by a multi-Bernoulli pdf. Data association based on the sum-product algorithm and recycling of Bernoulli components enable the detection and tracking of low-observable objects with limited computational resources. Our simulation results demonstrate a significantly improved tracking performance compared to a state-of-the-art TBD method.