Reward is not Necessary: How to Create a Compositional Self-Preserving Agent for Life-Long Learning

We introduce a physiological model-based agent as proof-of-principle that it is possible to define a flexible self-preserving system that does not use a reward signal or reward-maximization as an objective. We achieve this by introducing the Self-Preserving Agent (SPA) with a physiological structure where the system can get trapped in an absorbing state if the agent does not solve and execute goal-directed polices. Our agent is defined using new class of Bellman equations called Operator Bellman Equations (OBEs), for encoding jointly non-stationary non-Markovian tasks formalized as a Temporal Goal Markov Decision Process (TGMDP). OBEs produce optimal goal-conditioned spatiotemporal transition operators that map an initial state-time to the final state-times of a policy used to complete a goal, and can also be used to forecast future states in multiple dynamic physiological state-spaces. SPA is equipped with an intrinsic motivation function called the valence function, which quantifies the changes in empowerment (the channel capacity of a transition operator) after following a policy. Because empowerment is a function of a transition operator, there is a natural synergism between empowerment and OBEs: the OBEs create hierarchical transition operators, and the valence function can evaluate hierarchical empowerment change defined on these operators. The valence function can then be used for goal selection, wherein the agent chooses a policy sequence that realizes goal states which produce maximum empowerment gain. In doing so, the agent will seek freedom and avoid internal death-states that undermine its ability to control both external and internal states in the future, thereby exhibiting the capacity of predictive and anticipatory self-preservation. We also compare SPA to Multi-objective RL, and discuss its capacity for symbolic reasoning and life-long learning.

Jump Operator Planning: Goal-Conditioned Policy Ensembles and Zero-Shot Transfer

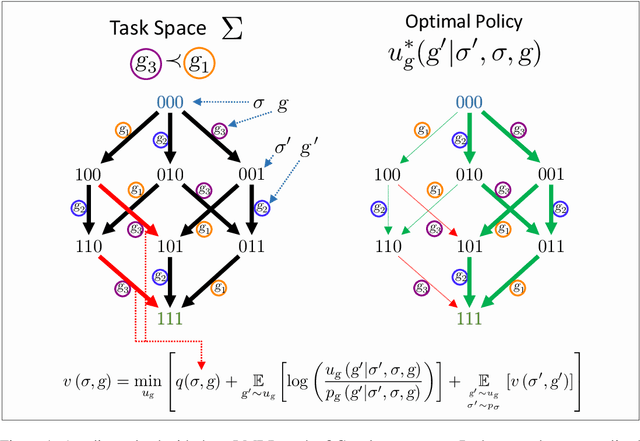
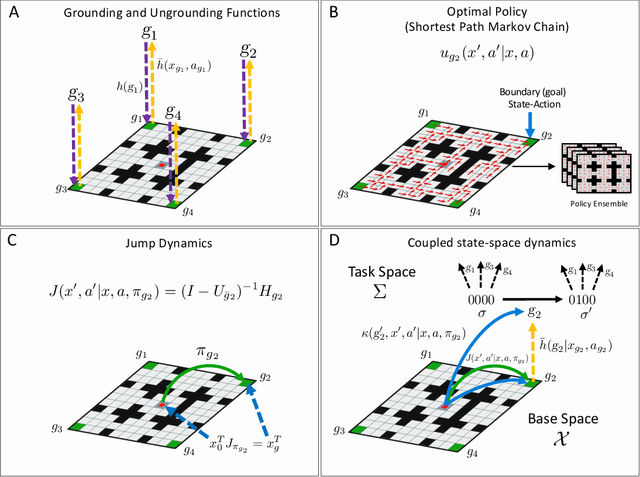
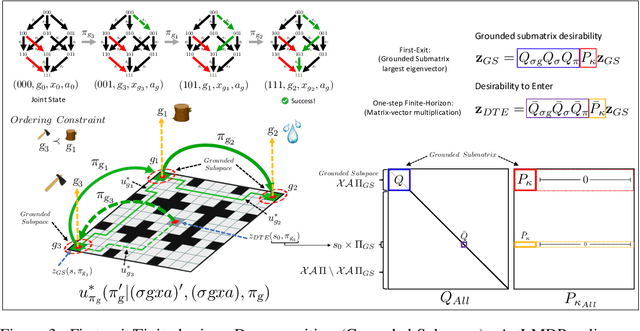
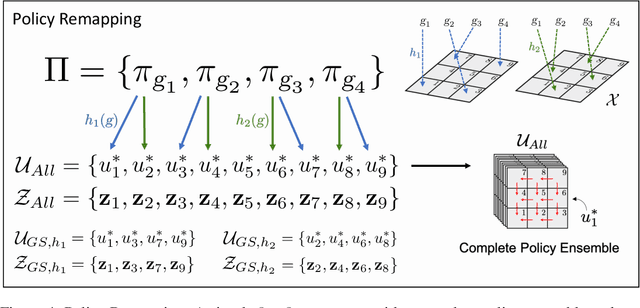
In Hierarchical Control, compositionality, abstraction, and task-transfer are crucial for designing versatile algorithms which can solve a variety of problems with maximal representational reuse. We propose a novel hierarchical and compositional framework called Jump-Operator Dynamic Programming for quickly computing solutions within a super-exponential space of sequential sub-goal tasks with ordering constraints, while also providing a fast linearly-solvable algorithm as an implementation. This approach involves controlling over an ensemble of reusable goal-conditioned polices functioning as temporally extended actions, and utilizes transition operators called feasibility functions, which are used to summarize initial-to-final state dynamics of the polices. Consequently, the added complexity of grounding a high-level task space onto a larger ambient state-space can be mitigated by optimizing in a lower-dimensional subspace defined by the grounding, substantially improving the scalability of the algorithm while effecting transferable solutions. We then identify classes of objective functions on this subspace whose solutions are invariant to the grounding, resulting in optimal zero-shot transfer.

Constraint Satisfaction Propagation: Non-stationary Policy Synthesis for Temporal Logic Planning

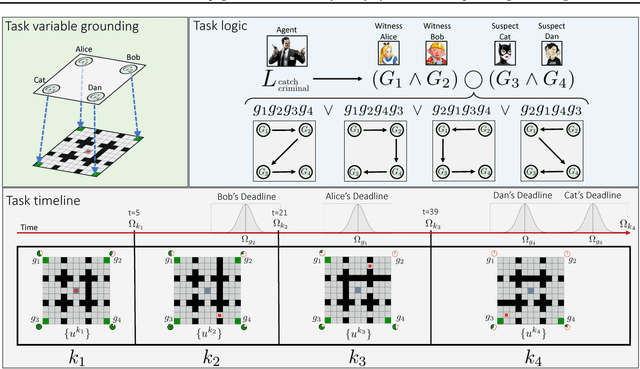
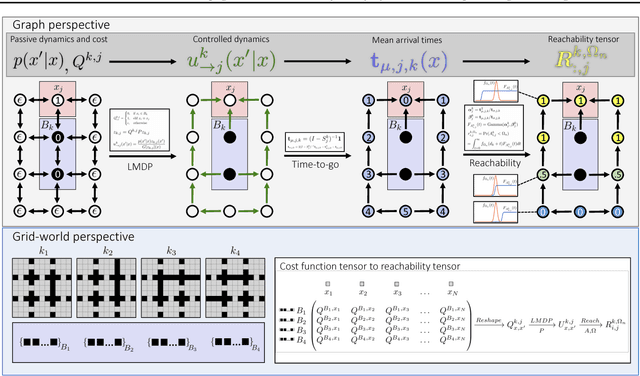
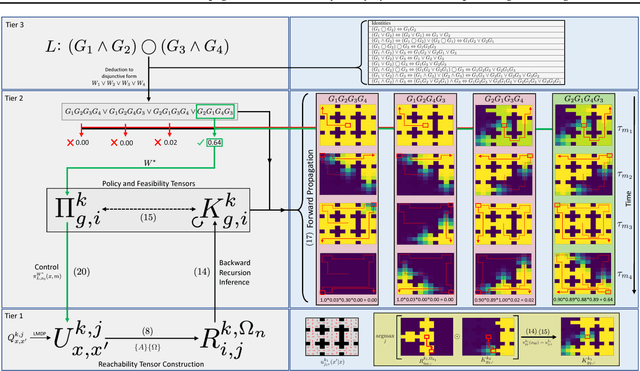
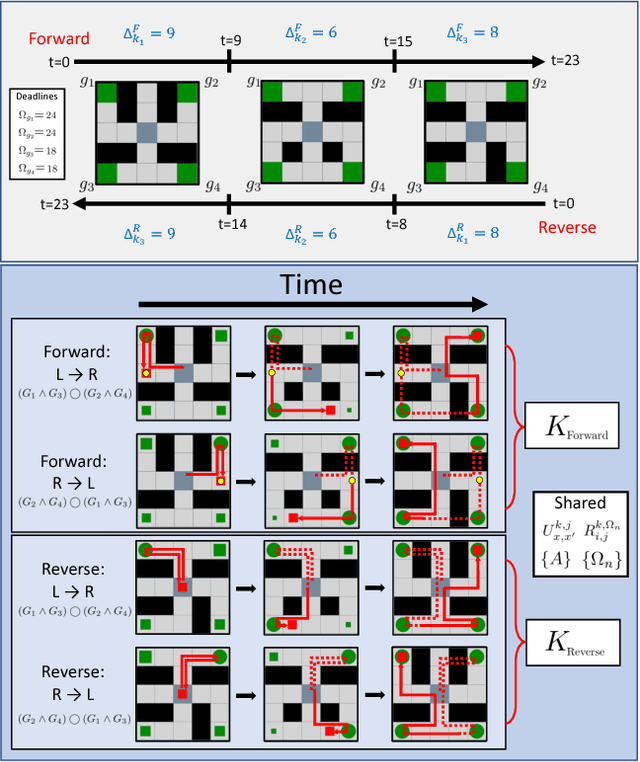
Problems arise when using reward functions to capture dependencies between sequential time-constrained goal states because the state-space must be prohibitively expanded to accommodate a history of successfully achieved sub-goals. Policies and value functions derived with stationarity assumptions are not readily decomposable, leading to a tension between reward maximization and task generalization. We demonstrate a logic-compatible approach using model-based knowledge of environment dynamics and deadline information to directly infer non-stationary policies composed of reusable stationary policies. The policies are constructed to maximize the probability of satisfying time-sensitive goals while respecting time-varying obstacles. Our approach explicitly maintains two different spaces, a high-level logical task specification where the task-variables are grounded onto the low-level state-space of a Markov decision process. Computing satisfiability at the task-level is made possible by a Bellman-like equation which operates on a tensor that links the temporal relationship between the two spaces; the equation solves for a value function that can be explicitly interpreted as the probability of sub-goal satisfaction under the synthesized non-stationary policy, an approach we term Constraint Satisfaction Propagation (CSP).