Jump Operator Planning: Goal-Conditioned Policy Ensembles and Zero-Shot Transfer
Paper and Code
Jul 06, 2020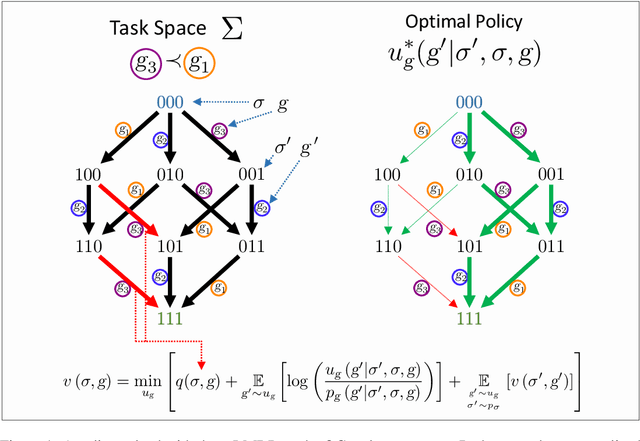
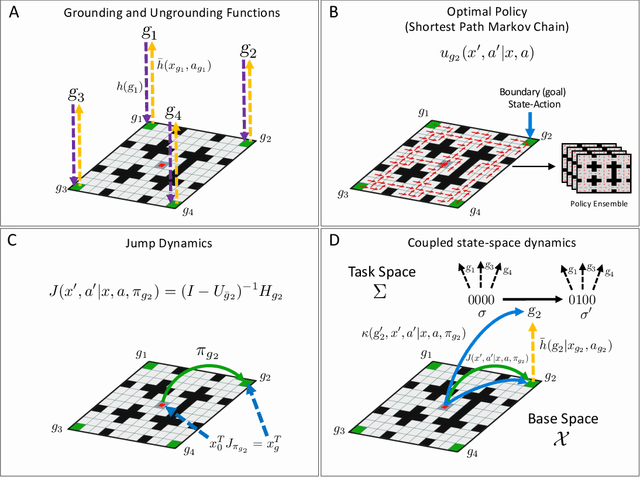
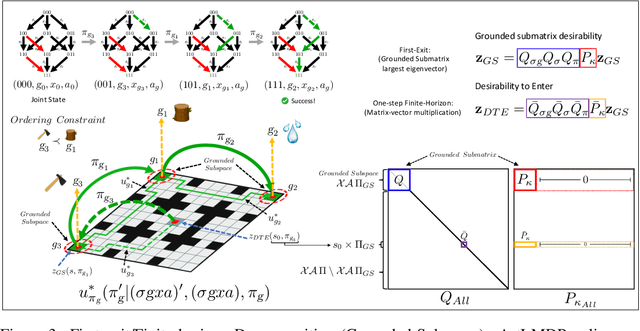
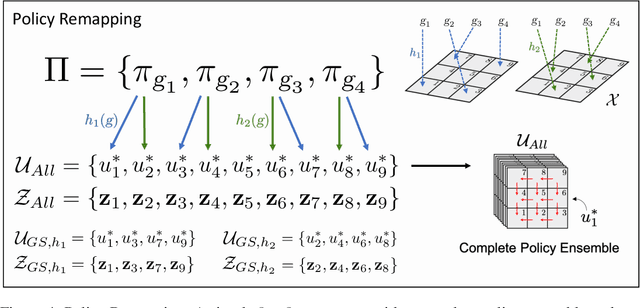
In Hierarchical Control, compositionality, abstraction, and task-transfer are crucial for designing versatile algorithms which can solve a variety of problems with maximal representational reuse. We propose a novel hierarchical and compositional framework called Jump-Operator Dynamic Programming for quickly computing solutions within a super-exponential space of sequential sub-goal tasks with ordering constraints, while also providing a fast linearly-solvable algorithm as an implementation. This approach involves controlling over an ensemble of reusable goal-conditioned polices functioning as temporally extended actions, and utilizes transition operators called feasibility functions, which are used to summarize initial-to-final state dynamics of the polices. Consequently, the added complexity of grounding a high-level task space onto a larger ambient state-space can be mitigated by optimizing in a lower-dimensional subspace defined by the grounding, substantially improving the scalability of the algorithm while effecting transferable solutions. We then identify classes of objective functions on this subspace whose solutions are invariant to the grounding, resulting in optimal zero-shot transfer.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge