Constraint Satisfaction Propagation: Non-stationary Policy Synthesis for Temporal Logic Planning
Paper and Code
Jan 30, 2019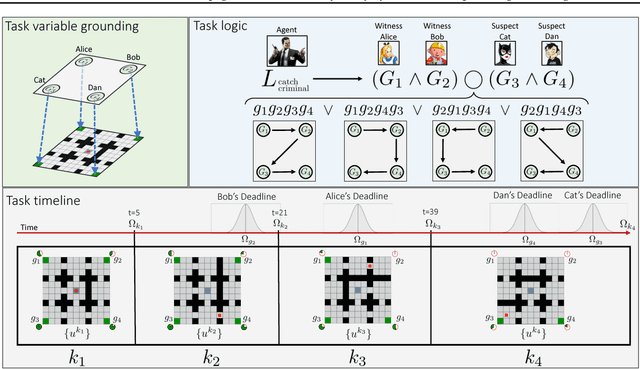
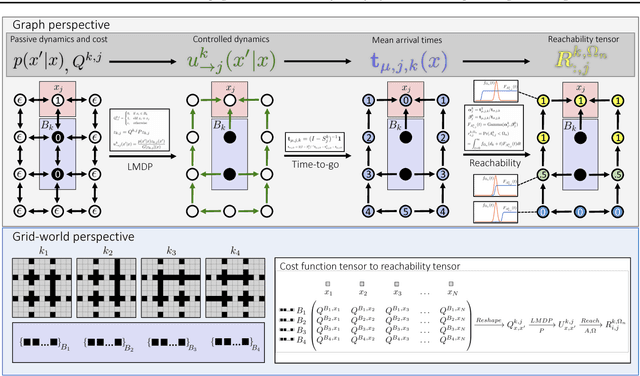
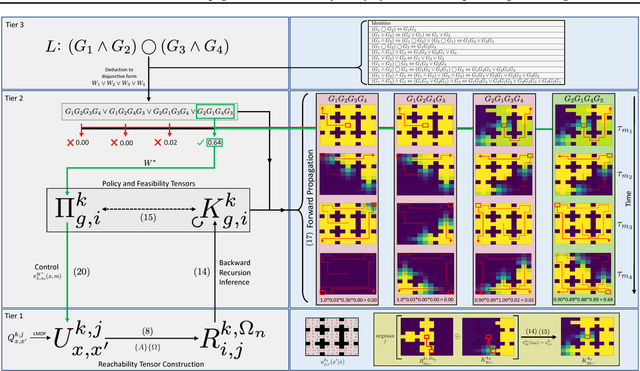
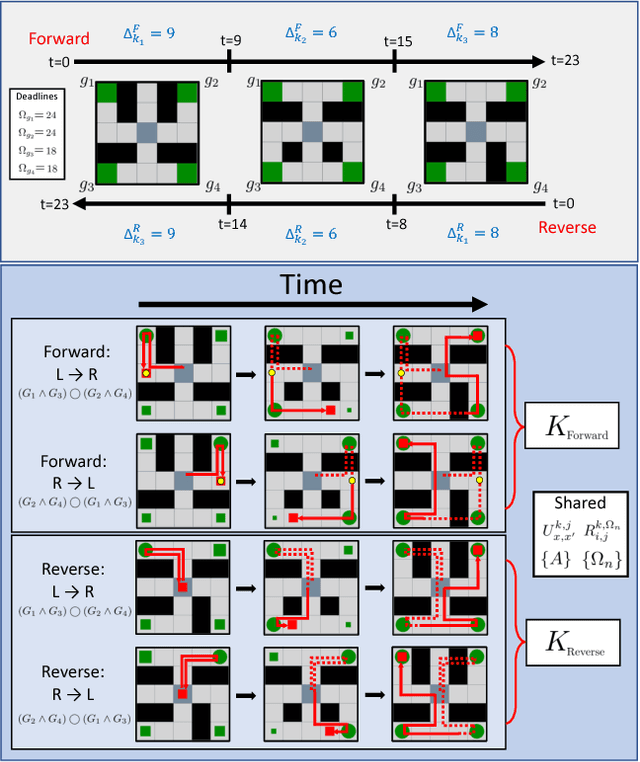
Problems arise when using reward functions to capture dependencies between sequential time-constrained goal states because the state-space must be prohibitively expanded to accommodate a history of successfully achieved sub-goals. Policies and value functions derived with stationarity assumptions are not readily decomposable, leading to a tension between reward maximization and task generalization. We demonstrate a logic-compatible approach using model-based knowledge of environment dynamics and deadline information to directly infer non-stationary policies composed of reusable stationary policies. The policies are constructed to maximize the probability of satisfying time-sensitive goals while respecting time-varying obstacles. Our approach explicitly maintains two different spaces, a high-level logical task specification where the task-variables are grounded onto the low-level state-space of a Markov decision process. Computing satisfiability at the task-level is made possible by a Bellman-like equation which operates on a tensor that links the temporal relationship between the two spaces; the equation solves for a value function that can be explicitly interpreted as the probability of sub-goal satisfaction under the synthesized non-stationary policy, an approach we term Constraint Satisfaction Propagation (CSP).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge