Single-component gradient rules for variational quantum algorithms

Many near-term quantum computing algorithms are conceived as variational quantum algorithms, in which parameterized quantum circuits are optimized in a hybrid quantum-classical setup. Examples are variational quantum eigensolvers, quantum approximate optimization algorithms as well as various algorithms in the context of quantum-assisted machine learning. A common bottleneck of any such algorithm is constituted by the optimization of the variational parameters. A popular set of optimization methods work on the estimate of the gradient, obtained by means of circuit evaluations. We will refer to the way in which one can combine these circuit evaluations as gradient rules. This work provides a comprehensive picture of the family of gradient rules that vary parameters of quantum gates individually. The most prominent known members of this family are the parameter shift rule and the finite differences method. To unite this family, we propose a generalized parameter shift rule that expresses all members of the aforementioned family as special cases, and discuss how all of these can be seen as providing access to a linear combination of exact first- and second-order derivatives. We further prove that a parameter shift rule with one non-shifted evaluation and only one shifted circuit evaluation can not exist does not exist, and introduce a novel perspective for approaching new gradient rules.

Training Quantum Embedding Kernels on Near-Term Quantum Computers

Kernel methods are a cornerstone of classical machine learning. The idea of using quantum computers to compute kernels has recently attracted attention. Quantum embedding kernels (QEKs) constructed by embedding data into the Hilbert space of a quantum computer are a particular quantum kernel technique that allows to gather insights into learning problems and that are particularly suitable for noisy intermediate-scale quantum devices. In this work, we first provide an accessible introduction to quantum embedding kernels and then analyze the practical issues arising when realizing them on a noisy near-term quantum computer. We focus on quantum embedding kernels with variational parameters. These variational parameters are optimized for a given dataset by increasing the kernel-target alignment, a heuristic connected to the achievable classification accuracy. We further show under which conditions noise from device imperfections influences the predicted kernel and provide a strategy to mitigate these detrimental effects which is tailored to quantum embedding kernels. We also address the influence of finite sampling and derive bounds that put guarantees on the quality of the kernel matrix. We illustrate our findings by numerical experiments and tests on actual hardware.

Evaluation of Parameterized Quantum Circuits: on the design, and the relation between classification accuracy, expressibility and entangling capability

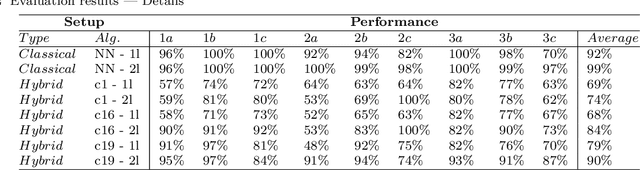
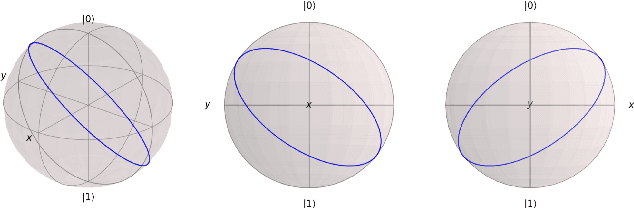
Quantum computers promise improvements in terms of both computational speedup and increased accuracy. Relevant areas are optimization, chemistry and machine learning, of which we will focus on the latter. Much of the prior art focuses on determining computational speedup, but how do we know if a particular quantum circuit shows promise for achieving high classification accuracy? Previous work by Sim et al. proposed descriptors to characterize and compare Parameterized Quantum Circuits. In this work, we will investigate any potential relation between the classification accuracy and two of these descriptors, being expressibility and entangling capability. We will first investigate different types of gates in quantum circuits and the changes they incur on the decision boundary. From this, we will propose design criteria for constructing circuits. We will also numerically compare the classifications performance of various quantum circuits and their quantified measure of expressibility and entangling capability, as derived in previous work. From this, we conclude that the common approach to layer combinations of rotational gates and conditional rotational gates provides the best accuracy. We also show that, for our experiments on a limited number of circuits, a coarse-grained relationship exists between entangling capability and classification accuracy, as well as a more fine-grained correlation between expressibility and classification accuracy. Future research will need to be performed to quantify this relation.

Integration and Evaluation of Quantum Accelerators for Data-Driven User Functions

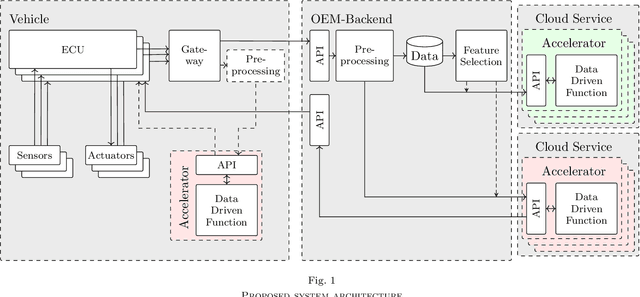
Quantum computers hold great promise for accelerating computationally challenging algorithms on noisy intermediate-scale quantum (NISQ) devices in the upcoming years. Much attention of the current research is directed to algorithmic research on artificial data that is disconnected from live systems, such as optimization of systems or training of learning algorithms. In this paper we investigate the integration of quantum systems into industry-grade system architectures. In this work we propose a system architecture for the integration of quantum accelerators. In order to evaluate our proposed system architecture we implemented various algorithms including a classical system, a gate-based quantum accelerator and a quantum annealer. This algorithm automates user habits using data-driven functions trained on real-world data. This also includes an evaluation of the quantum enhanced kernel, that previously was only evaluated on artificial data. In our evaluation, we showed that the quantum-enhanced kernel performs at least equally well to a classical state-of-the-art kernel. We also showed a low reduction in accuracy and latency numbers within acceptable bounds when running on the gate-based IBM quantum accelerator. We, therefore, conclude it is feasible to integrate NISQ-era devices in industry-grade system architecture in preparation for future hardware improvements.