Generalized Multi-Speed Dubins Motion Model

The paper develops a novel motion model, called Generalized Multi-Speed Dubins Motion Model (GMDM), which extends the Dubins model by considering multiple speeds. While the Dubins model produces time-optimal paths under a constant-speed constraint, these paths could be suboptimal if this constraint is relaxed to include multiple speeds. This is because a constant speed results in a large minimum turning radius, thus producing paths with longer maneuvers and larger travel times. In contrast, multi-speed relaxation allows for slower speed sharp turns, thus producing more direct paths with shorter maneuvers and smaller travel times. Furthermore, the inability of the Dubins model to reduce speed could result in fast maneuvers near obstacles, thus producing paths with high collision risks. In this regard, GMDM provides the motion planners the ability to jointly optimize time and risk by allowing the change of speed along the path. GMDM is built upon the six Dubins path types considering the change of speed on path segments. It is theoretically established that GMDM provides full reachability of the configuration space for any speed selections. Furthermore, it is shown that the Dubins model is a specific case of GMDM for constant speeds. The solutions of GMDM are analytical and suitable for real-time applications. The performance of GMDM in terms of solution quality (i.e., time/time-risk cost) and computation time is comparatively evaluated against the existing motion models in obstacle-free as well as obstacle-rich environments via extensive Monte Carlo simulations. The results show that in obstacle-free environments, GMDM produces near time-optimal paths with significantly lower travel times than the Dubins model while having similar computation times. In obstacle-rich environments, GMDM produces time-risk optimized paths with substantially lower collision risks.

T$^{\star}$-Lite: A Fast Time-Risk Optimal Motion Planning Algorithm for Multi-Speed Autonomous Vehicles

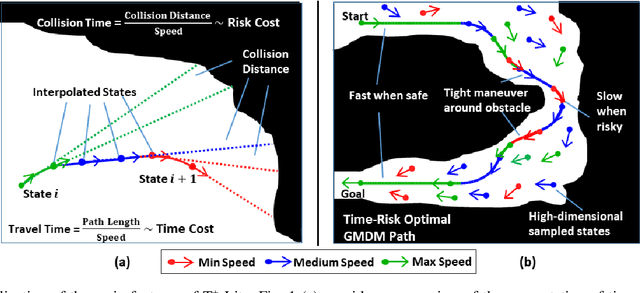
In this paper, we develop a new algorithm, called T$^{\star}$-Lite, that enables fast time-risk optimal motion planning for variable-speed autonomous vehicles. The T$^{\star}$-Lite algorithm is a significantly faster version of the previously developed T$^{\star}$ algorithm. T$^{\star}$-Lite uses the novel time-risk cost function of T$^{\star}$; however, instead of a grid-based approach, it uses an asymptotically optimal sampling-based motion planner. Furthermore, it utilizes the recently developed Generalized Multi-speed Dubins Motion-model (GMDM) for sample-to-sample kinodynamic motion planning. The sample-based approach and GMDM significantly reduce the computational burden of T$^{\star}$ while providing reasonable solution quality. The sample points are drawn from a four-dimensional configuration space consisting of two position coordinates plus vehicle heading and speed. Specifically, T$^{\star}$-Lite enables the motion planner to select the vehicle speed and direction based on its proximity to the obstacle to generate faster and safer paths. In this paper, T$^{\star}$-Lite is developed using the RRT$^{\star}$ motion planner, but adaptation to other motion planners is straightforward and depends on the needs of the planner

Rapid Motion-Planning for Dubins Vehicles under Environmental Drifts

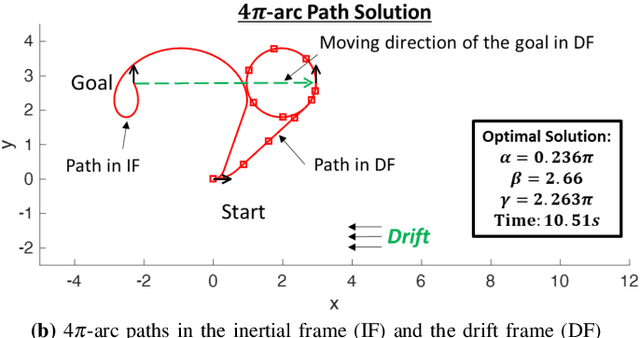
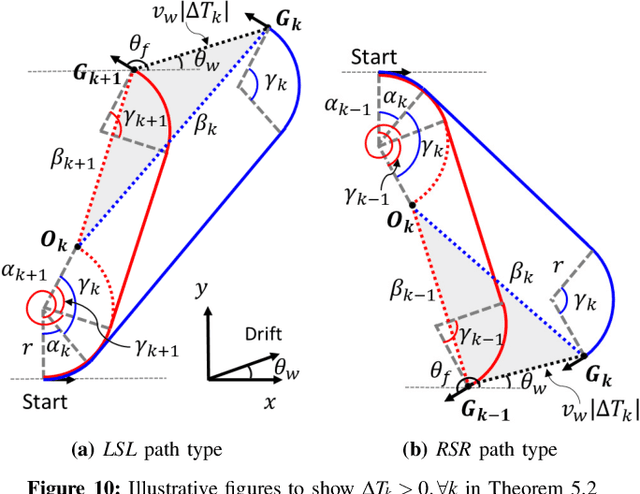
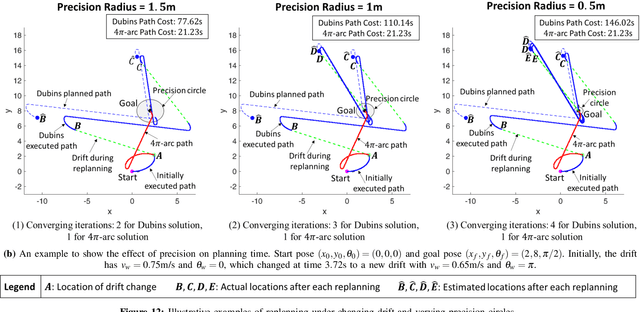
This paper presents a rapid (i.e., (near) real time) solution to the minimum-time motion planning problem for Dubins vehicles under environmental drifts (e.g., wind or ocean currents). Real-time solutions are essential in time-critical situations (e.g., replanning under dynamically changing environments or tracking fast moving targets). Typically, Dubins problem requires to solve for six path types; however, due to the presence of drifts, four of these path types require to solve the root-finding problem involving transcendental functions. Thus, the existing solution methods result in high computation times and their applicability for real-time applications is limited. In this regard, in order to obtain a (near) real-time solution, this paper proposes a novel approach where only a subset of two Dubins path types (i.e., LSL and RSR) are used which have direct analytical solutions in the presence of drifts. We show that by extending the feasible range of circular arcs in these path types: 1) full reachability of any goal pose is guaranteed, and 2) even better paths can be produced with lower time costs. Theoretical findings are comparatively evaluated by extensive Monte-Carlo simulations.