Rapid Motion-Planning for Dubins Vehicles under Environmental Drifts

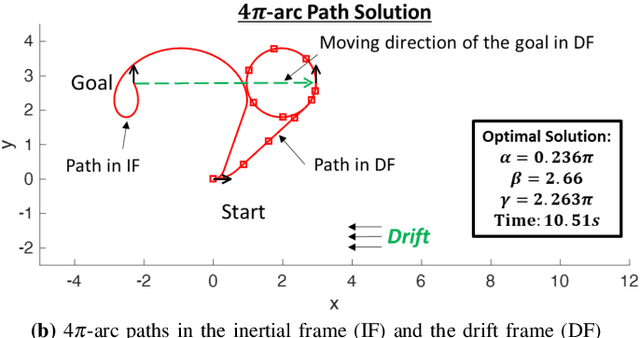
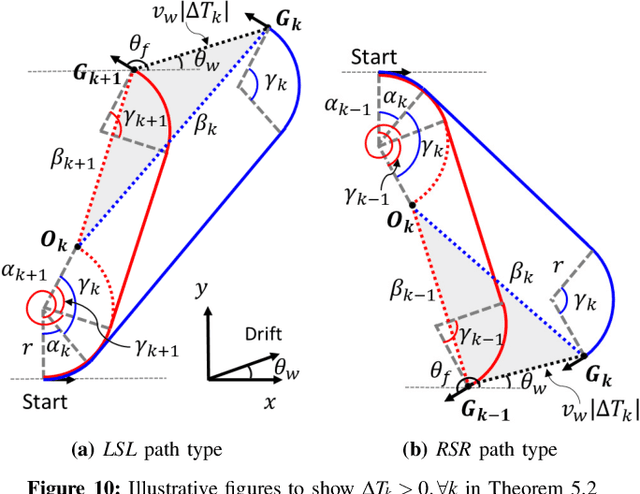
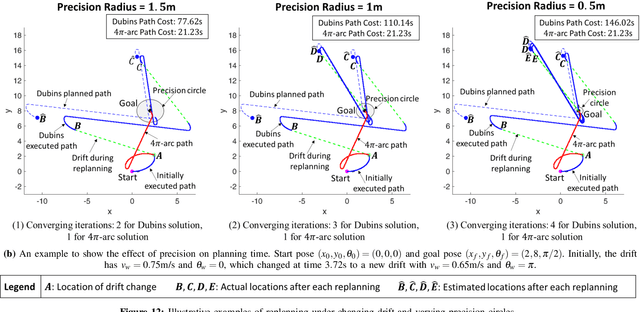
This paper presents a rapid (i.e., (near) real time) solution to the minimum-time motion planning problem for Dubins vehicles under environmental drifts (e.g., wind or ocean currents). Real-time solutions are essential in time-critical situations (e.g., replanning under dynamically changing environments or tracking fast moving targets). Typically, Dubins problem requires to solve for six path types; however, due to the presence of drifts, four of these path types require to solve the root-finding problem involving transcendental functions. Thus, the existing solution methods result in high computation times and their applicability for real-time applications is limited. In this regard, in order to obtain a (near) real-time solution, this paper proposes a novel approach where only a subset of two Dubins path types (i.e., LSL and RSR) are used which have direct analytical solutions in the presence of drifts. We show that by extending the feasible range of circular arcs in these path types: 1) full reachability of any goal pose is guaranteed, and 2) even better paths can be produced with lower time costs. Theoretical findings are comparatively evaluated by extensive Monte-Carlo simulations.