Thierry Roncalli
Improving the Robustness of Trading Strategy Backtesting with Boltzmann Machines and Generative Adversarial Networks
Jul 09, 2020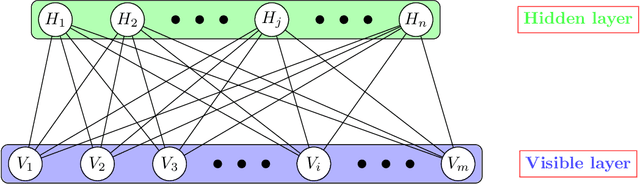
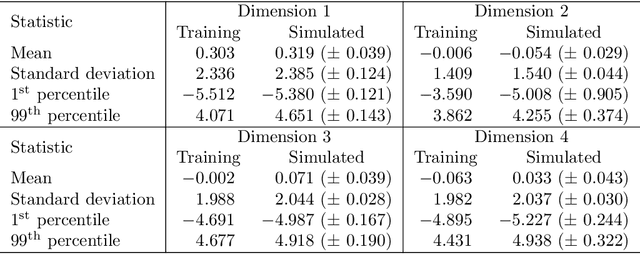
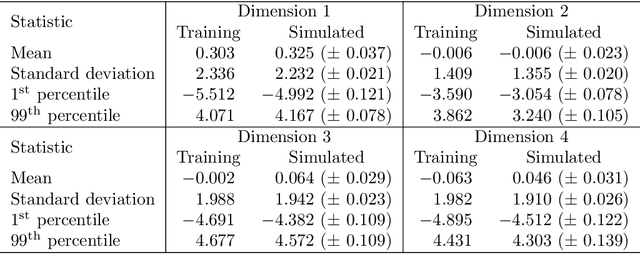
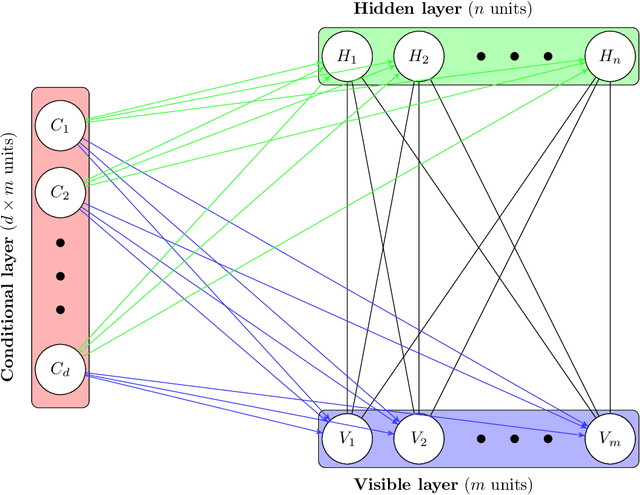
Abstract:This article explores the use of machine learning models to build a market generator. The underlying idea is to simulate artificial multi-dimensional financial time series, whose statistical properties are the same as those observed in the financial markets. In particular, these synthetic data must preserve the probability distribution of asset returns, the stochastic dependence between the different assets and the autocorrelation across time. The article proposes then a new approach for estimating the probability distribution of backtest statistics. The final objective is to develop a framework for improving the risk management of quantitative investment strategies, in particular in the space of smart beta, factor investing and alternative risk premia.
A Note on Portfolio Optimization with Quadratic Transaction Costs
Jan 06, 2020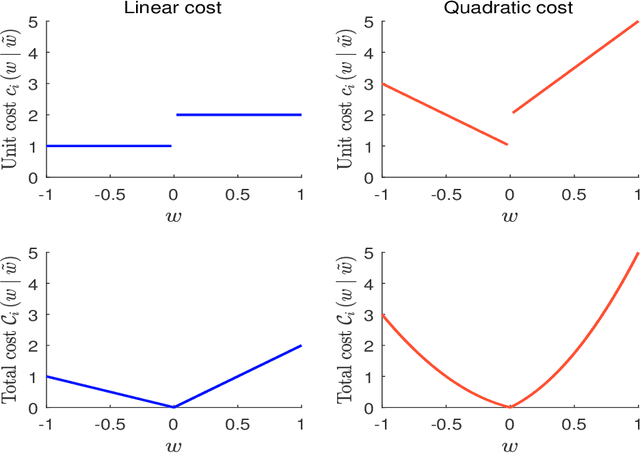
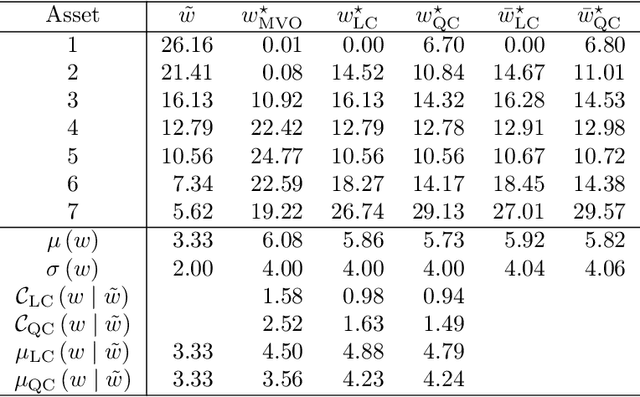
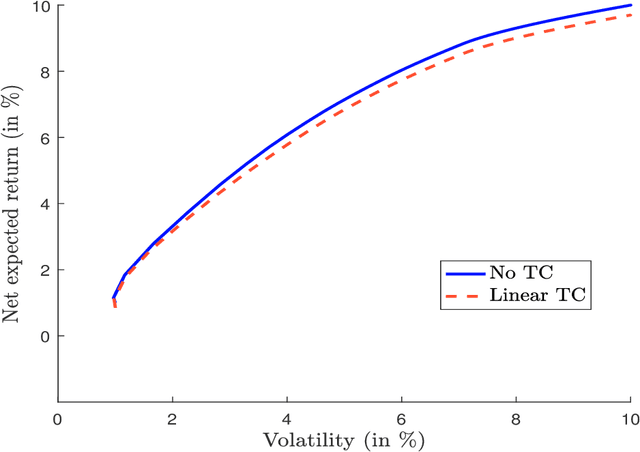
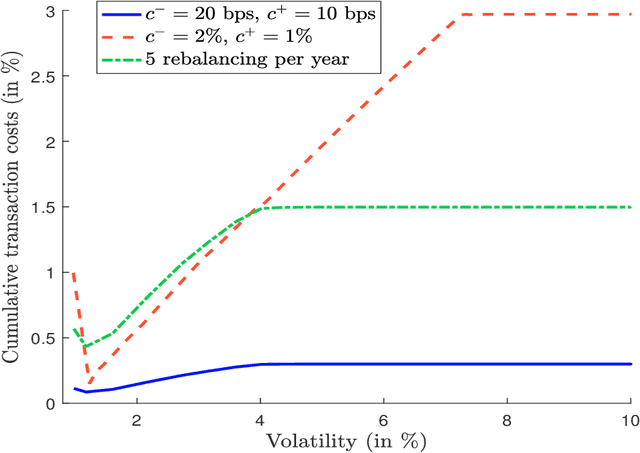
Abstract:In this short note, we consider mean-variance optimized portfolios with transaction costs. We show that introducing quadratic transaction costs makes the optimization problem more difficult than using linear transaction costs. The reason lies in the specification of the budget constraint, which is no longer linear. We provide numerical algorithms for solving this issue and illustrate how transaction costs may considerably impact the expected returns of optimized portfolios.
Machine Learning Optimization Algorithms & Portfolio Allocation
Sep 23, 2019



Abstract:Portfolio optimization emerged with the seminal paper of Markowitz (1952). The original mean-variance framework is appealing because it is very efficient from a computational point of view. However, it also has one well-established failing since it can lead to portfolios that are not optimal from a financial point of view. Nevertheless, very few models have succeeded in providing a real alternative solution to the Markowitz model. The main reason lies in the fact that most academic portfolio optimization models are intractable in real life although they present solid theoretical properties. By intractable we mean that they can be implemented for an investment universe with a small number of assets using a lot of computational resources and skills, but they are unable to manage a universe with dozens or hundreds of assets. However, the emergence and the rapid development of robo-advisors means that we need to rethink portfolio optimization and go beyond the traditional mean-variance optimization approach. Another industry has faced similar issues concerning large-scale optimization problems. Machine learning has long been associated with linear and logistic regression models. Again, the reason was the inability of optimization algorithms to solve high-dimensional industrial problems. Nevertheless, the end of the 1990s marked an important turning point with the development and the rediscovery of several methods that have since produced impressive results. The goal of this paper is to show how portfolio allocation can benefit from the development of these large-scale optimization algorithms. Not all of these algorithms are useful in our case, but four of them are essential when solving complex portfolio optimization problems. These four algorithms are the coordinate descent, the alternating direction method of multipliers, the proximal gradient method and the Dykstra's algorithm.
Financial Applications of Gaussian Processes and Bayesian Optimization
Mar 12, 2019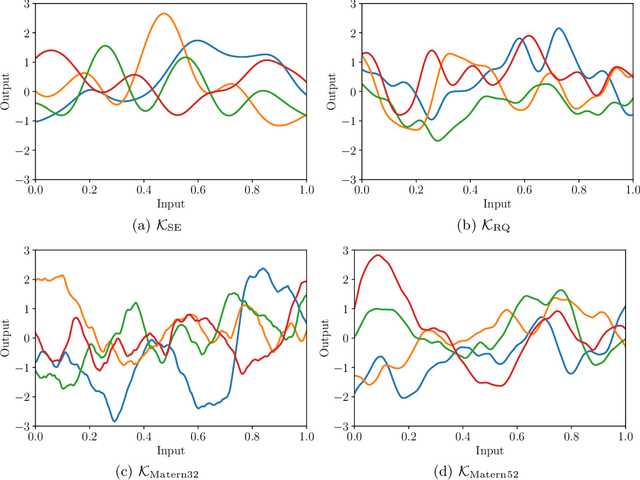

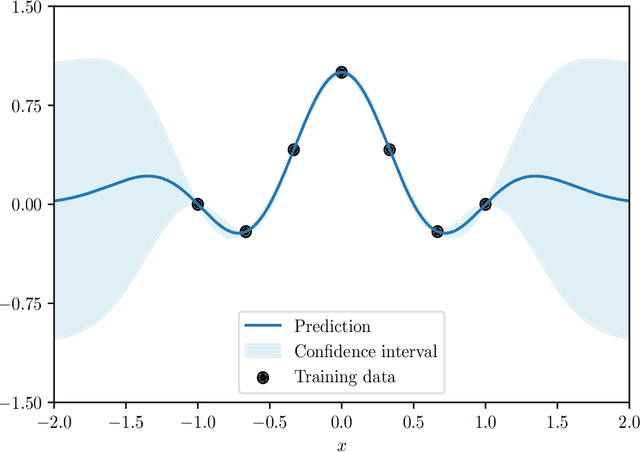

Abstract:In the last five years, the financial industry has been impacted by the emergence of digitalization and machine learning. In this article, we explore two methods that have undergone rapid development in recent years: Gaussian processes and Bayesian optimization. Gaussian processes can be seen as a generalization of Gaussian random vectors and are associated with the development of kernel methods. Bayesian optimization is an approach for performing derivative-free global optimization in a small dimension, and uses Gaussian processes to locate the global maximum of a black-box function. The first part of the article reviews these two tools and shows how they are connected. In particular, we focus on the Gaussian process regression, which is the core of Bayesian machine learning, and the issue of hyperparameter selection. The second part is dedicated to two financial applications. We first consider the modeling of the term structure of interest rates. More precisely, we test the fitting method and compare the GP prediction and the random walk model. The second application is the construction of trend-following strategies, in particular the online estimation of trend and covariance windows.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge