DP-XGBoost: Private Machine Learning at Scale

The big-data revolution announced ten years ago does not seem to have fully happened at the expected scale. One of the main obstacle to this, has been the lack of data circulation. And one of the many reasons people and organizations did not share as much as expected is the privacy risk associated with data sharing operations. There has been many works on practical systems to compute statistical queries with Differential Privacy (DP). There have also been practical implementations of systems to train Neural Networks with DP, but relatively little efforts have been dedicated to designing scalable classical Machine Learning (ML) models providing DP guarantees. In this work we describe and implement a DP fork of a battle tested ML model: XGBoost. Our approach beats by a large margin previous attempts at the task, in terms of accuracy achieved for a given privacy budget. It is also the only DP implementation of boosted trees that scales to big data and can run in distributed environments such as: Kubernetes, Dask or Apache Spark.

Financial Applications of Gaussian Processes and Bayesian Optimization

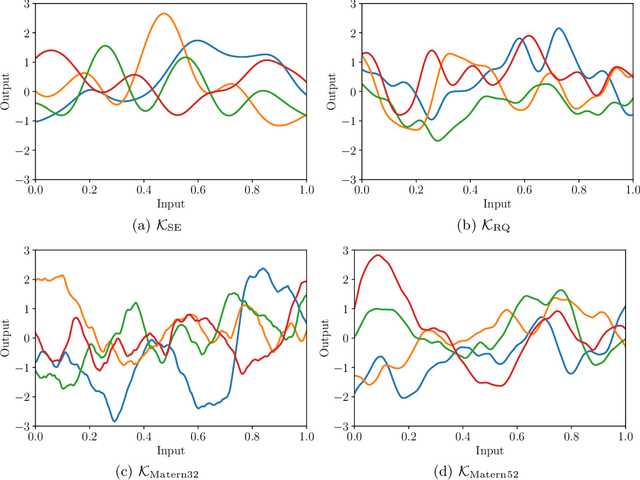
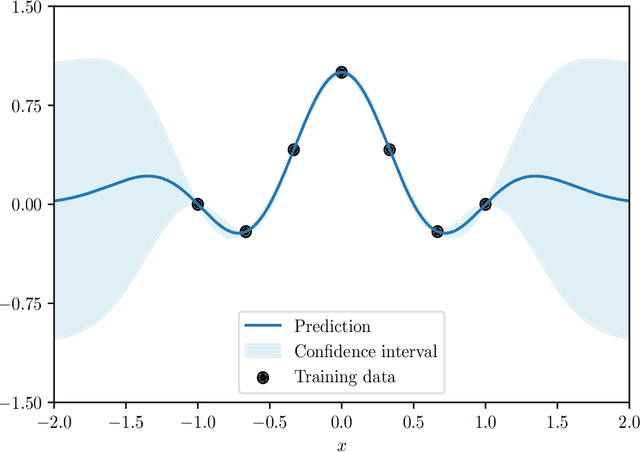
In the last five years, the financial industry has been impacted by the emergence of digitalization and machine learning. In this article, we explore two methods that have undergone rapid development in recent years: Gaussian processes and Bayesian optimization. Gaussian processes can be seen as a generalization of Gaussian random vectors and are associated with the development of kernel methods. Bayesian optimization is an approach for performing derivative-free global optimization in a small dimension, and uses Gaussian processes to locate the global maximum of a black-box function. The first part of the article reviews these two tools and shows how they are connected. In particular, we focus on the Gaussian process regression, which is the core of Bayesian machine learning, and the issue of hyperparameter selection. The second part is dedicated to two financial applications. We first consider the modeling of the term structure of interest rates. More precisely, we test the fitting method and compare the GP prediction and the random walk model. The second application is the construction of trend-following strategies, in particular the online estimation of trend and covariance windows.