A Goal-Directed Implementation of Query Answering for Hybrid MKNF Knowledge Bases

Ontologies and rules are usually loosely coupled in knowledge representation formalisms. In fact, ontologies use open-world reasoning while the leading semantics for rules use non-monotonic, closed-world reasoning. One exception is the tightly-coupled framework of Minimal Knowledge and Negation as Failure (MKNF), which allows statements about individuals to be jointly derived via entailment from an ontology and inferences from rules. Nonetheless, the practical usefulness of MKNF has not always been clear, although recent work has formalized a general resolution-based method for querying MKNF when rules are taken to have the well-founded semantics, and the ontology is modeled by a general oracle. That work leaves open what algorithms should be used to relate the entailments of the ontology and the inferences of rules. In this paper we provide such algorithms, and describe the implementation of a query-driven system, CDF-Rules, for hybrid knowledge bases combining both (non-monotonic) rules under the well-founded semantics and a (monotonic) ontology, represented by a CDF Type-1 (ALQ) theory. To appear in Theory and Practice of Logic Programming (TPLP)

Query-driven Procedures for Hybrid MKNF Knowledge Bases

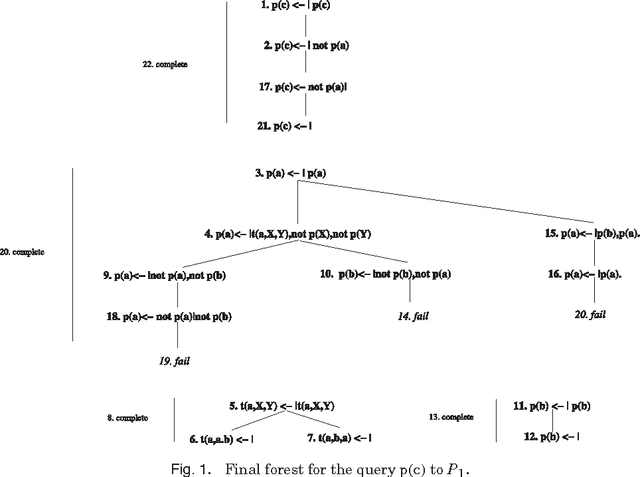
Hybrid MKNF knowledge bases are one of the most prominent tightly integrated combinations of open-world ontology languages with closed-world (non-monotonic) rule paradigms. The definition of Hybrid MKNF is parametric on the description logic (DL) underlying the ontology language, in the sense that non-monotonic rules can extend any decidable DL language. Two related semantics have been defined for Hybrid MKNF: one that is based on the Stable Model Semantics for logic programs and one on the Well-Founded Semantics (WFS). Under WFS, the definition of Hybrid MKNF relies on a bottom-up computation that has polynomial data complexity whenever the DL language is tractable. Here we define a general query-driven procedure for Hybrid MKNF that is sound with respect to the stable model-based semantics, and sound and complete with respect to its WFS variant. This procedure is able to answer a slightly restricted form of conjunctive queries, and is based on tabled rule evaluation extended with an external oracle that captures reasoning within the ontology. Such an (abstract) oracle receives as input a query along with knowledge already derived, and replies with a (possibly empty) set of atoms, defined in the rules, whose truth would suffice to prove the initial query. With appropriate assumptions on the complexity of the abstract oracle, the general procedure maintains the data complexity of the WFS for Hybrid MKNF knowledge bases. To illustrate this approach, we provide a concrete oracle for EL+, a fragment of the light-weight DL EL++. Such an oracle has practical use, as EL++ is the language underlying OWL 2 EL, which is part of the W3C recommendations for the Semantic Web, and is tractable for reasoning tasks such as subsumption. We show that query-driven Hybrid MKNF preserves polynomial data complexity when using the EL+ oracle and WFS.

Well-Definedness and Efficient Inference for Probabilistic Logic Programming under the Distribution Semantics

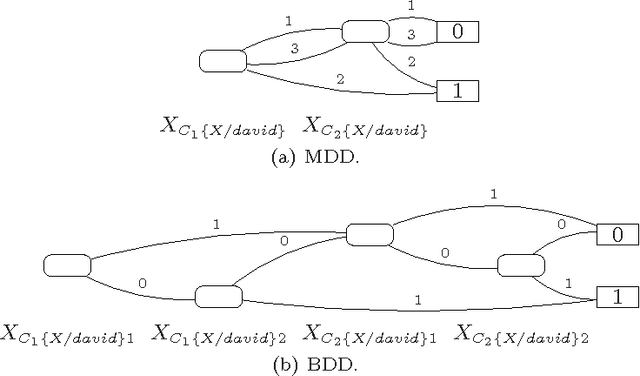
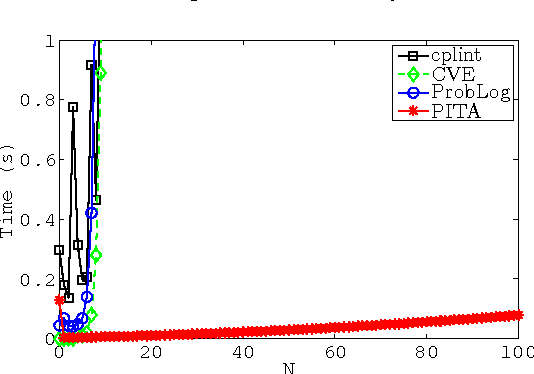
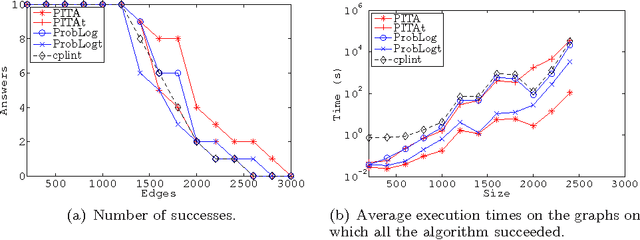
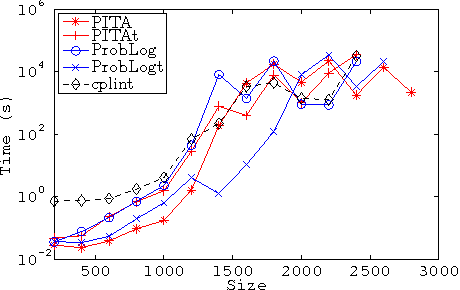
The distribution semantics is one of the most prominent approaches for the combination of logic programming and probability theory. Many languages follow this semantics, such as Independent Choice Logic, PRISM, pD, Logic Programs with Annotated Disjunctions (LPADs) and ProbLog. When a program contains functions symbols, the distribution semantics is well-defined only if the set of explanations for a query is finite and so is each explanation. Well-definedness is usually either explicitly imposed or is achieved by severely limiting the class of allowed programs. In this paper we identify a larger class of programs for which the semantics is well-defined together with an efficient procedure for computing the probability of queries. Since LPADs offer the most general syntax, we present our results for them, but our results are applicable to all languages under the distribution semantics. We present the algorithm "Probabilistic Inference with Tabling and Answer subsumption" (PITA) that computes the probability of queries by transforming a probabilistic program into a normal program and then applying SLG resolution with answer subsumption. PITA has been implemented in XSB and tested on six domains: two with function symbols and four without. The execution times are compared with those of ProbLog, cplint and CVE, PITA was almost always able to solve larger problems in a shorter time, on domains with and without function symbols.

The PITA System: Tabling and Answer Subsumption for Reasoning under Uncertainty

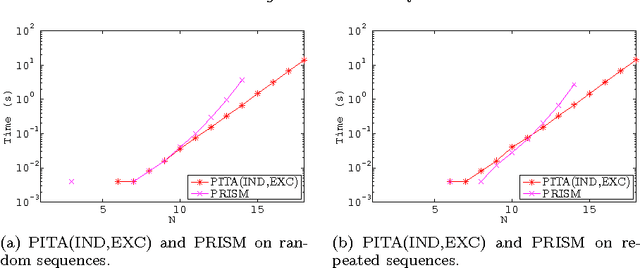
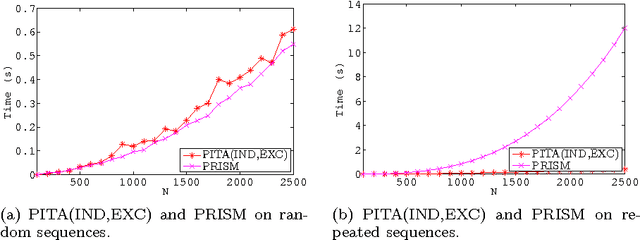
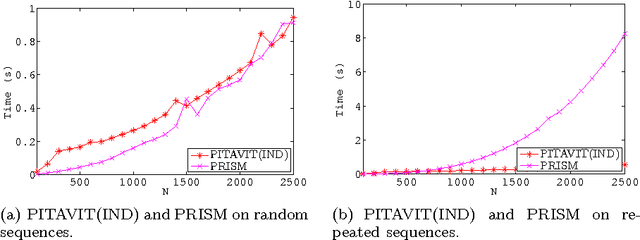
Many real world domains require the representation of a measure of uncertainty. The most common such representation is probability, and the combination of probability with logic programs has given rise to the field of Probabilistic Logic Programming (PLP), leading to languages such as the Independent Choice Logic, Logic Programs with Annotated Disjunctions (LPADs), Problog, PRISM and others. These languages share a similar distribution semantics, and methods have been devised to translate programs between these languages. The complexity of computing the probability of queries to these general PLP programs is very high due to the need to combine the probabilities of explanations that may not be exclusive. As one alternative, the PRISM system reduces the complexity of query answering by restricting the form of programs it can evaluate. As an entirely different alternative, Possibilistic Logic Programs adopt a simpler metric of uncertainty than probability. Each of these approaches -- general PLP, restricted PLP, and Possibilistic Logic Programming -- can be useful in different domains depending on the form of uncertainty to be represented, on the form of programs needed to model problems, and on the scale of the problems to be solved. In this paper, we show how the PITA system, which originally supported the general PLP language of LPADs, can also efficiently support restricted PLP and Possibilistic Logic Programs. PITA relies on tabling with answer subsumption and consists of a transformation along with an API for library functions that interface with answer subsumption.

Splitting and Updating Hybrid Knowledge Bases (Extended Version)

Over the years, nonmonotonic rules have proven to be a very expressive and useful knowledge representation paradigm. They have recently been used to complement the expressive power of Description Logics (DLs), leading to the study of integrative formal frameworks, generally referred to as hybrid knowledge bases, where both DL axioms and rules can be used to represent knowledge. The need to use these hybrid knowledge bases in dynamic domains has called for the development of update operators, which, given the substantially different way Description Logics and rules are usually updated, has turned out to be an extremely difficult task. In [SL10], a first step towards addressing this problem was taken, and an update operator for hybrid knowledge bases was proposed. Despite its significance -- not only for being the first update operator for hybrid knowledge bases in the literature, but also because it has some applications - this operator was defined for a restricted class of problems where only the ABox was allowed to change, which considerably diminished its applicability. Many applications that use hybrid knowledge bases in dynamic scenarios require both DL axioms and rules to be updated. In this paper, motivated by real world applications, we introduce an update operator for a large class of hybrid knowledge bases where both the DL component as well as the rule component are allowed to dynamically change. We introduce splitting sequences and splitting theorem for hybrid knowledge bases, use them to define a modular update semantics, investigate its basic properties, and illustrate its use on a realistic example about cargo imports.

Abduction in Well-Founded Semantics and Generalized Stable Models

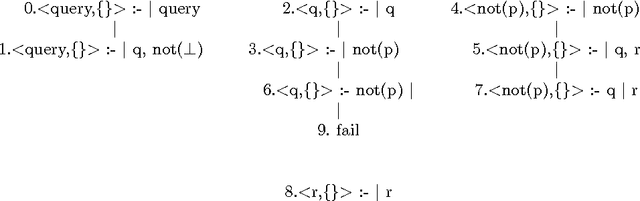
Abductive logic programming offers a formalism to declaratively express and solve problems in areas such as diagnosis, planning, belief revision and hypothetical reasoning. Tabled logic programming offers a computational mechanism that provides a level of declarativity superior to that of Prolog, and which has supported successful applications in fields such as parsing, program analysis, and model checking. In this paper we show how to use tabled logic programming to evaluate queries to abductive frameworks with integrity constraints when these frameworks contain both default and explicit negation. The result is the ability to compute abduction over well-founded semantics with explicit negation and answer sets. Our approach consists of a transformation and an evaluation method. The transformation adjoins to each objective literal $O$ in a program, an objective literal $not(O)$ along with rules that ensure that $not(O)$ will be true if and only if $O$ is false. We call the resulting program a {\em dual} program. The evaluation method, \wfsmeth, then operates on the dual program. \wfsmeth{} is sound and complete for evaluating queries to abductive frameworks whose entailment method is based on either the well-founded semantics with explicit negation, or on answer sets. Further, \wfsmeth{} is asymptotically as efficient as any known method for either class of problems. In addition, when abduction is not desired, \wfsmeth{} operating on a dual program provides a novel tabling method for evaluating queries to ground extended programs whose complexity and termination properties are similar to those of the best tabling methods for the well-founded semantics. A publicly available meta-interpreter has been developed for \wfsmeth{} using the XSB system.