Contextual Abductive Reasoning with Side-Effects

The belief bias effect is a phenomenon which occurs when we think that we judge an argument based on our reasoning, but are actually influenced by our beliefs and prior knowledge. Evans, Barston and Pollard carried out a psychological syllogistic reasoning task to prove this effect. Participants were asked whether they would accept or reject a given syllogism. We discuss one specific case which is commonly assumed to be believable but which is actually not logically valid. By introducing abnormalities, abduction and background knowledge, we adequately model this case under the weak completion semantics. Our formalization reveals new questions about possible extensions in abductive reasoning. For instance, observations and their explanations might include some relevant prior abductive contextual information concerning some side-effect or leading to a contestable or refutable side-effect. A weaker notion indicates the support of some relevant consequences by a prior abductive context. Yet another definition describes jointly supported relevant consequences, which captures the idea of two observations containing mutually supportive side-effects. Though motivated with and exemplified by the running psychology application, the various new general abductive context definitions are introduced here and given a declarative semantics for the first time, and have a much wider scope of application. Inspection points, a concept introduced by Pereira and Pinto, allows us to express these definitions syntactically and intertwine them into an operational semantics.

Properties of Stable Model Semantics Extensions

The stable model (SM) semantics lacks the properties of existence, relevance and cumulativity. If we prospectively consider the class of conservative extensions of SM semantics (i.e., semantics that for each normal logic program P retrieve a superset of the set of stable models of P), one may wander how do the semantics of this class behave in what concerns the aforementioned properties. That is the type of issue dealt with in this paper. We define a large class of conservative extensions of the SM semantics, dubbed affix stable model semantics, ASM, and study the above referred properties into two non-disjoint subfamilies of the class ASM, here dubbed ASMh and ASMm. From this study a number of results stem which facilitate the assessment of semantics in the class ASMh U ASMm with respect to the properties of existence, relevance and cumulativity, whilst unveiling relations among these properties. As a result of the approach taken in our work, light is shed on the characterization of the SM semantics, as we show that the properties of (lack of) existence and (lack of) cautious monotony are equivalent, which opposes statements on this issue that may be found in the literature; we also characterize the relevance failure of SM semantics in a more clear way than usually stated in the literature.

Joint Tabling of Logic Program Abductions and Updates

Abductive logic programs offer a formalism to declaratively represent and reason about problems in a variety of areas: diagnosis, decision making, hypothetical reasoning, etc. On the other hand, logic program updates allow us to express knowledge changes, be they internal (or self) and external (or world) changes. Abductive logic programs and logic program updates thus naturally coexist in problems that are susceptible to hypothetical reasoning about change. Taking this as a motivation, in this paper we integrate abductive logic programs and logic program updates by jointly exploiting tabling features of logic programming. The integration is based on and benefits from the two implementation techniques we separately devised previously, viz., tabled abduction and incremental tabling for query-driven propagation of logic program updates. A prototype of the integrated system is implemented in XSB Prolog.

Abduction in Well-Founded Semantics and Generalized Stable Models

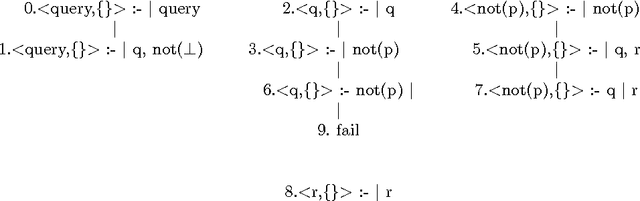
Abductive logic programming offers a formalism to declaratively express and solve problems in areas such as diagnosis, planning, belief revision and hypothetical reasoning. Tabled logic programming offers a computational mechanism that provides a level of declarativity superior to that of Prolog, and which has supported successful applications in fields such as parsing, program analysis, and model checking. In this paper we show how to use tabled logic programming to evaluate queries to abductive frameworks with integrity constraints when these frameworks contain both default and explicit negation. The result is the ability to compute abduction over well-founded semantics with explicit negation and answer sets. Our approach consists of a transformation and an evaluation method. The transformation adjoins to each objective literal $O$ in a program, an objective literal $not(O)$ along with rules that ensure that $not(O)$ will be true if and only if $O$ is false. We call the resulting program a {\em dual} program. The evaluation method, \wfsmeth, then operates on the dual program. \wfsmeth{} is sound and complete for evaluating queries to abductive frameworks whose entailment method is based on either the well-founded semantics with explicit negation, or on answer sets. Further, \wfsmeth{} is asymptotically as efficient as any known method for either class of problems. In addition, when abduction is not desired, \wfsmeth{} operating on a dual program provides a novel tabling method for evaluating queries to ground extended programs whose complexity and termination properties are similar to those of the best tabling methods for the well-founded semantics. A publicly available meta-interpreter has been developed for \wfsmeth{} using the XSB system.