Error Distribution Smoothing:Advancing Low-Dimensional Imbalanced Regression

In real-world regression tasks, datasets frequently exhibit imbalanced distributions, characterized by a scarcity of data in high-complexity regions and an abundance in low-complexity areas. This imbalance presents significant challenges for existing classification methods with clear class boundaries, while highlighting a scarcity of approaches specifically designed for imbalanced regression problems. To better address these issues, we introduce a novel concept of Imbalanced Regression, which takes into account both the complexity of the problem and the density of data points, extending beyond traditional definitions that focus only on data density. Furthermore, we propose Error Distribution Smoothing (EDS) as a solution to tackle imbalanced regression, effectively selecting a representative subset from the dataset to reduce redundancy while maintaining balance and representativeness. Through several experiments, EDS has shown its effectiveness, and the related code and dataset can be accessed at https://anonymous.4open.science/r/Error-Distribution-Smoothing-762F.

Adviser-Actor-Critic: Eliminating Steady-State Error in Reinforcement Learning Control

High-precision control tasks present substantial challenges for reinforcement learning (RL) algorithms, frequently resulting in suboptimal performance attributed to network approximation inaccuracies and inadequate sample quality.These issues are exacerbated when the task requires the agent to achieve a precise goal state, as is common in robotics and other real-world applications.We introduce Adviser-Actor-Critic (AAC), designed to address the precision control dilemma by combining the precision of feedback control theory with the adaptive learning capability of RL and featuring an Adviser that mentors the actor to refine control actions, thereby enhancing the precision of goal attainment.Finally, through benchmark tests, AAC outperformed standard RL algorithms in precision-critical, goal-conditioned tasks, demonstrating AAC's high precision, reliability, and robustness.Code are available at: https://anonymous.4open.science/r/Adviser-Actor-Critic-8AC5.

Recursive Gaussian Process State Space Model

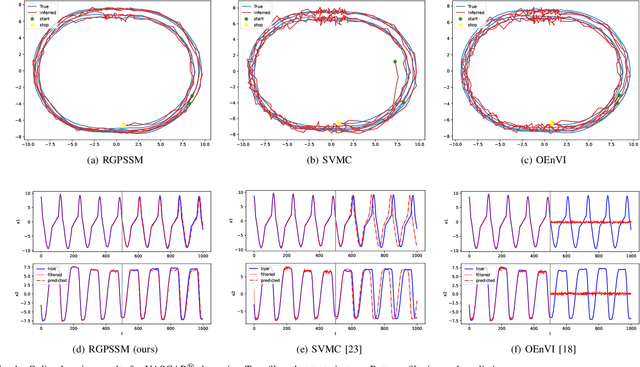
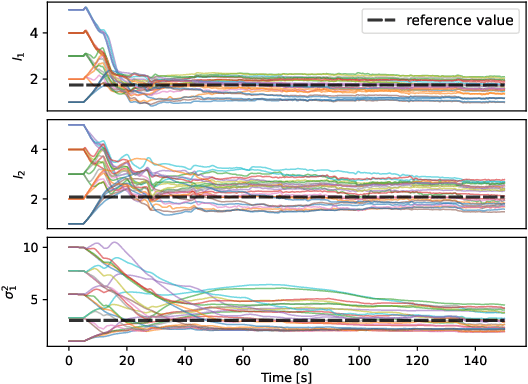
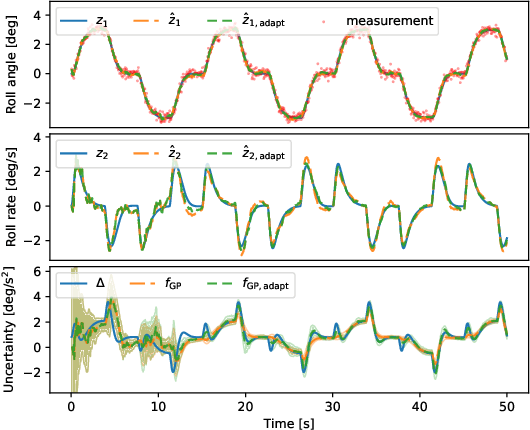
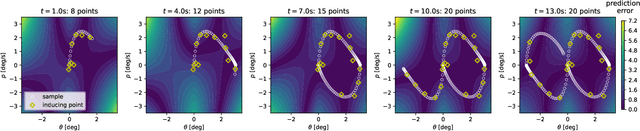
Learning dynamical models from data is not only fundamental but also holds great promise for advancing principle discovery, time-series prediction, and controller design. Among various approaches, Gaussian Process State-Space Models (GPSSMs) have recently gained significant attention due to their combination of flexibility and interpretability. However, for online learning, the field lacks an efficient method suitable for scenarios where prior information regarding data distribution and model function is limited. To address this issue, this paper proposes a recursive GPSSM method with adaptive capabilities for both operating domains and Gaussian process (GP) hyperparameters. Specifically, we first utilize first-order linearization to derive a Bayesian update equation for the joint distribution between the system state and the GP model, enabling closed-form and domain-independent learning. Second, an online selection algorithm for inducing points is developed based on informative criteria to achieve lightweight learning. Third, to support online hyperparameter optimization, we recover historical measurement information from the current filtering distribution. Comprehensive evaluations on both synthetic and real-world datasets demonstrate the superior accuracy, computational efficiency, and adaptability of our method compared to state-of-the-art online GPSSM techniques.