Recursive Gaussian Process State Space Model

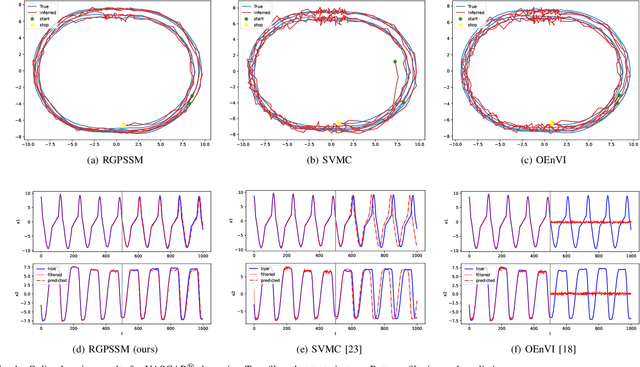
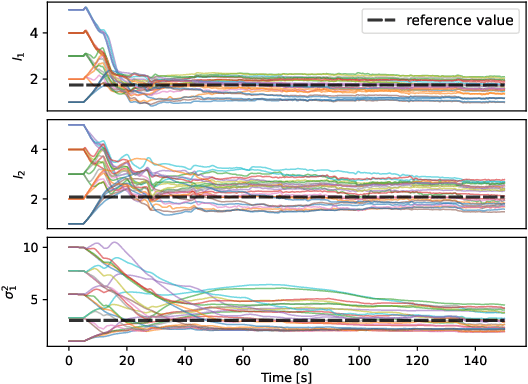
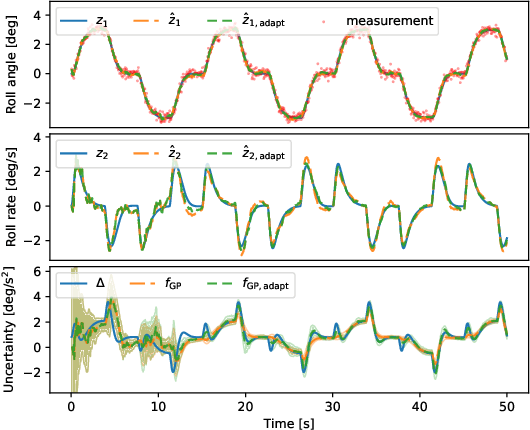
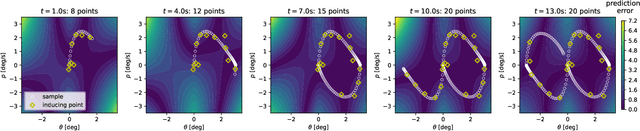
Learning dynamical models from data is not only fundamental but also holds great promise for advancing principle discovery, time-series prediction, and controller design. Among various approaches, Gaussian Process State-Space Models (GPSSMs) have recently gained significant attention due to their combination of flexibility and interpretability. However, for online learning, the field lacks an efficient method suitable for scenarios where prior information regarding data distribution and model function is limited. To address this issue, this paper proposes a recursive GPSSM method with adaptive capabilities for both operating domains and Gaussian process (GP) hyperparameters. Specifically, we first utilize first-order linearization to derive a Bayesian update equation for the joint distribution between the system state and the GP model, enabling closed-form and domain-independent learning. Second, an online selection algorithm for inducing points is developed based on informative criteria to achieve lightweight learning. Third, to support online hyperparameter optimization, we recover historical measurement information from the current filtering distribution. Comprehensive evaluations on both synthetic and real-world datasets demonstrate the superior accuracy, computational efficiency, and adaptability of our method compared to state-of-the-art online GPSSM techniques.

Solar-Sail Trajectory Design of Multiple Near Earth Asteroids Exploration Based on Deep Neural Network

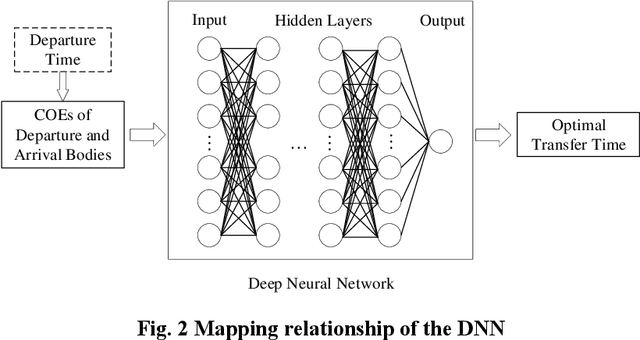
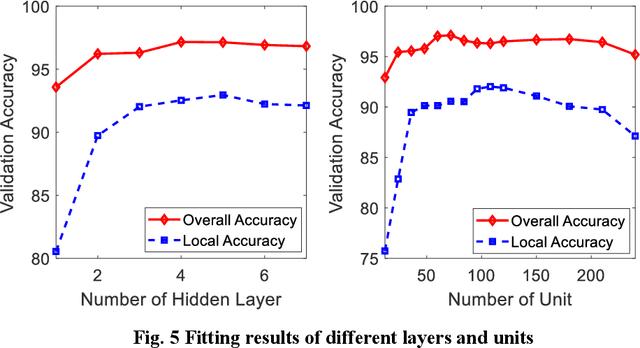
In the preliminary trajectory design of the multi-target rendezvous problem, a model that can quickly estimate the cost of the orbital transfer is essential. The estimation of the transfer time using solar sail between two arbitrary orbits is difficult and usually requires to solve an optimal control problem. Inspired by the successful applications of the deep neural network in nonlinear regression, this work explores the possibility and effectiveness of mapping the transfer time for solar sail from the orbital characteristics using the deep neural network. Furthermore, the Monte Carlo Tree Search method is investigated and used to search the optimal sequence considering a multi-asteroid exploration problem. The obtained sequences from preliminary design will be solved and verified by sequentially solving the optimal control problem. Two examples of different application backgrounds validate the effectiveness of the proposed approach.