Consistency between ordering and clustering methods for graphs

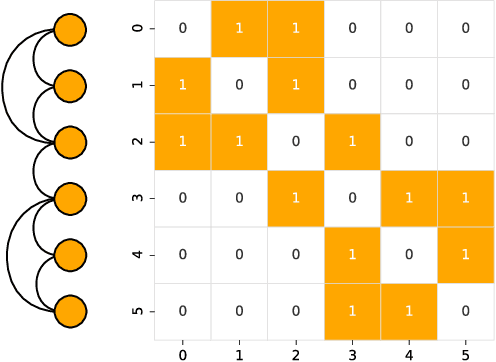
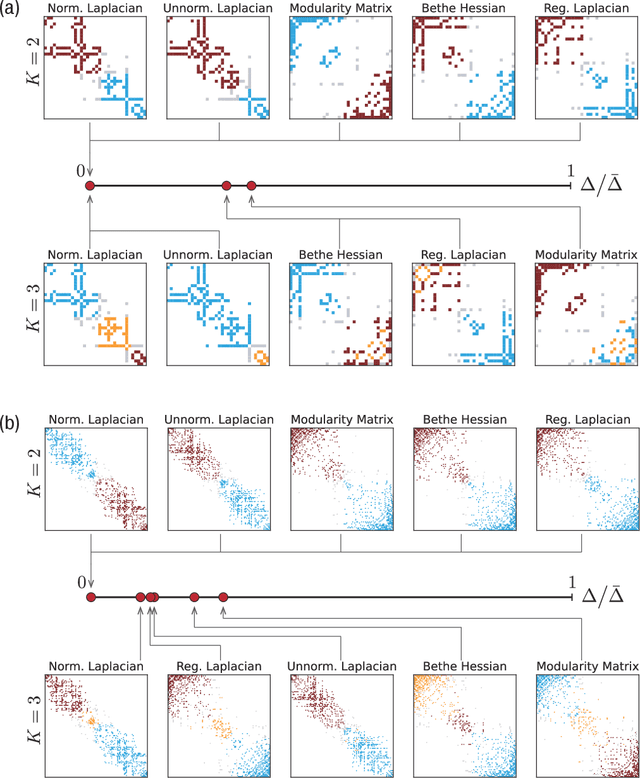
A relational dataset is often analyzed by optimally assigning a label to each element through clustering or ordering. While similar characterizations of a dataset would be achieved by both clustering and ordering methods, the former has been studied much more actively than the latter, particularly for the data represented as graphs. This study fills this gap by investigating methodological relationships between several clustering and ordering methods, focusing on spectral techniques. Furthermore, we evaluate the resulting performance of the clustering and ordering methods. To this end, we propose a measure called the label continuity error, which generically quantifies the degree of consistency between a sequence and partition for a set of elements. Based on synthetic and real-world datasets, we evaluate the extents to which an ordering method identifies a module structure and a clustering method identifies a banded structure.

Mean-field theory of graph neural networks in graph partitioning

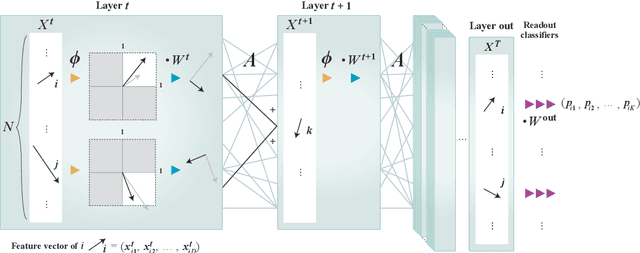
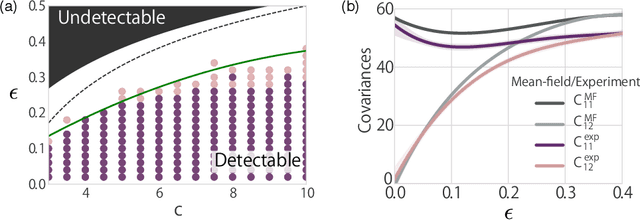
A theoretical performance analysis of the graph neural network (GNN) is presented. For classification tasks, the neural network approach has the advantage in terms of flexibility that it can be employed in a data-driven manner, whereas Bayesian inference requires the assumption of a specific model. A fundamental question is then whether GNN has a high accuracy in addition to this flexibility. Moreover, whether the achieved performance is predominately a result of the backpropagation or the architecture itself is a matter of considerable interest. To gain a better insight into these questions, a mean-field theory of a minimal GNN architecture is developed for the graph partitioning problem. This demonstrates a good agreement with numerical experiments.

Algorithmic detectability threshold of the stochastic block model

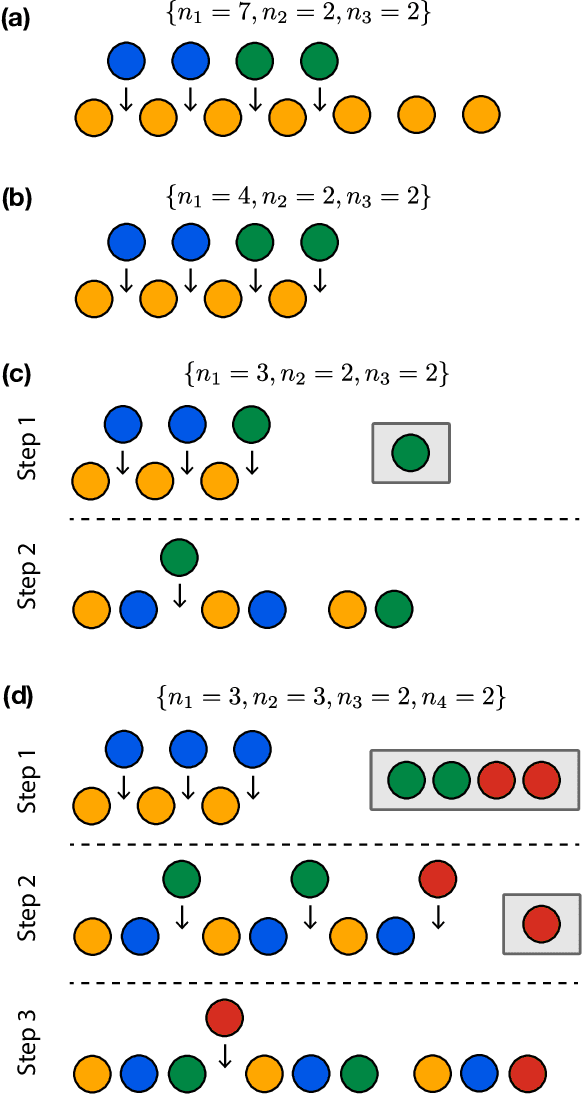
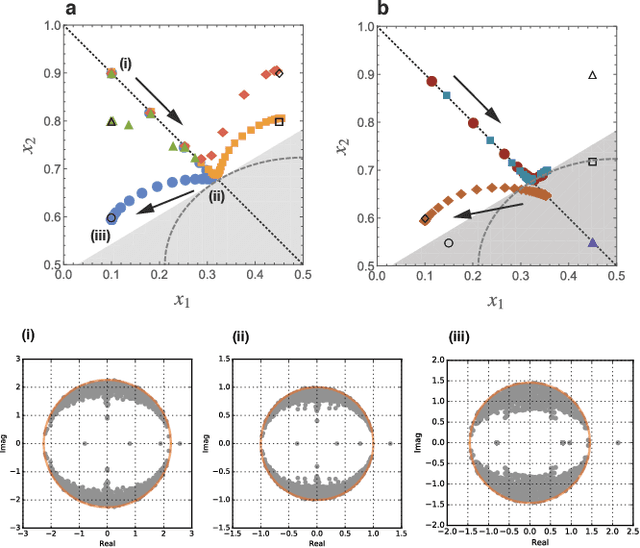
The assumption that the values of model parameters are known or correctly learned, i.e., the Nishimori condition, is one of the requirements for the detectability analysis of the stochastic block model in statistical inference. In practice, however, there is no example demonstrating that we can know the model parameters beforehand, and there is no guarantee that the model parameters can be learned accurately. In this study, we consider the expectation--maximization (EM) algorithm with belief propagation (BP) and derive its algorithmic detectability threshold. Our analysis is not restricted to the community structure, but includes general modular structures. Because the algorithm cannot always learn the planted model parameters correctly, the algorithmic detectability threshold is qualitatively different from the one with the Nishimori condition.

Algorithmic infeasibility of community detection in higher-order networks

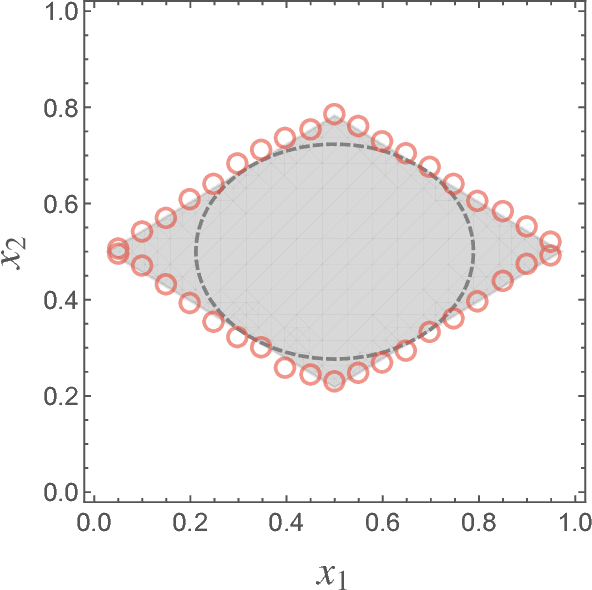
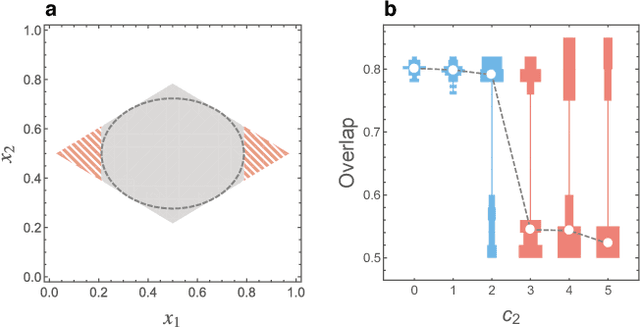
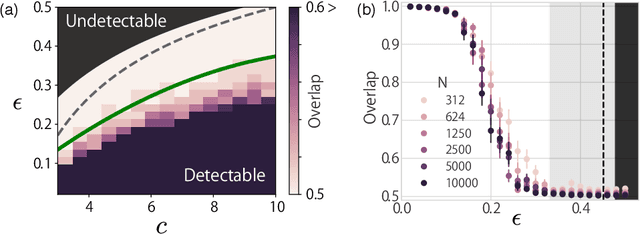
In principle, higher-order networks that have multiple edge types are more informative than their lower-order counterparts. In practice, however, excessively rich information may be algorithmically infeasible to extract. It requires an algorithm that assumes a high-dimensional model and such an algorithm may perform poorly or be extremely sensitive to the initial estimate of the model parameters. Herein, we address this problem of community detection through a detectability analysis. We focus on the expectation-maximization (EM) algorithm with belief propagation (BP), and analytically derive its algorithmic detectability threshold, i.e., the limit of the modular structure strength below which the algorithm can no longer detect any modular structures. The results indicate the existence of a phase in which the community detection of a lower-order network outperforms its higher-order counterpart.

A Tractable Fully Bayesian Method for the Stochastic Block Model

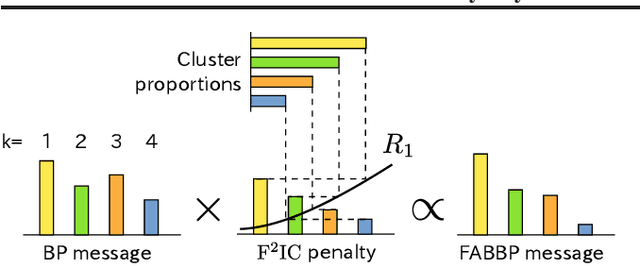
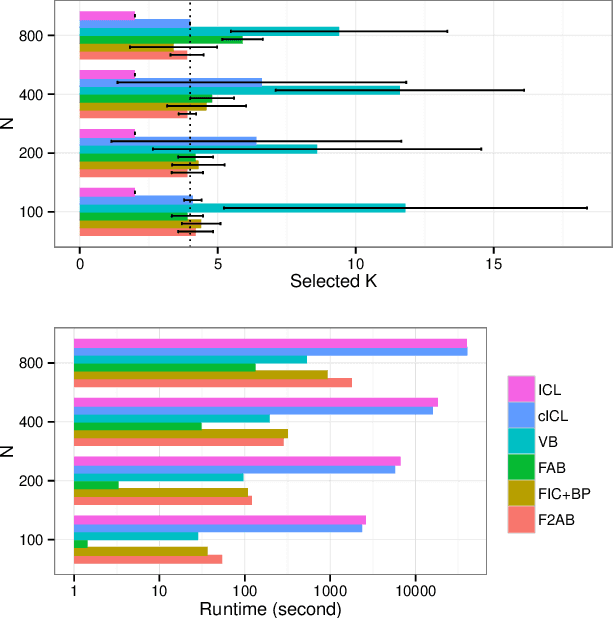
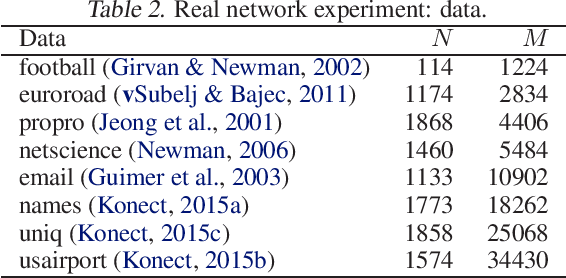
The stochastic block model (SBM) is a generative model revealing macroscopic structures in graphs. Bayesian methods are used for (i) cluster assignment inference and (ii) model selection for the number of clusters. In this paper, we study the behavior of Bayesian inference in the SBM in the large sample limit. Combining variational approximation and Laplace's method, a consistent criterion of the fully marginalized log-likelihood is established. Based on that, we derive a tractable algorithm that solves tasks (i) and (ii) concurrently, obviating the need for an outer loop to check all model candidates. Our empirical and theoretical results demonstrate that our method is scalable in computation, accurate in approximation, and concise in model selection.