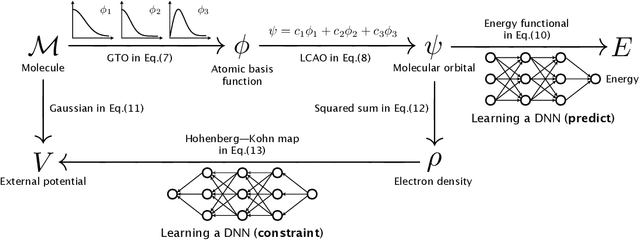
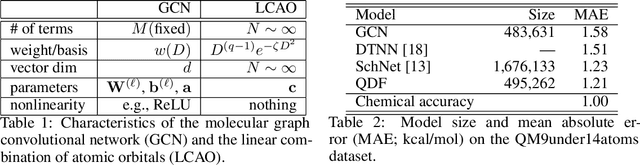
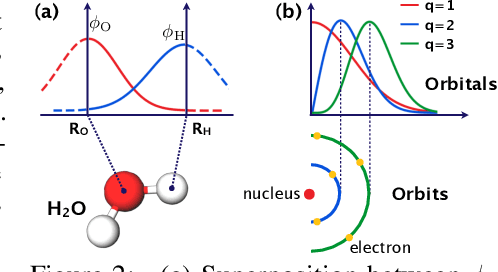
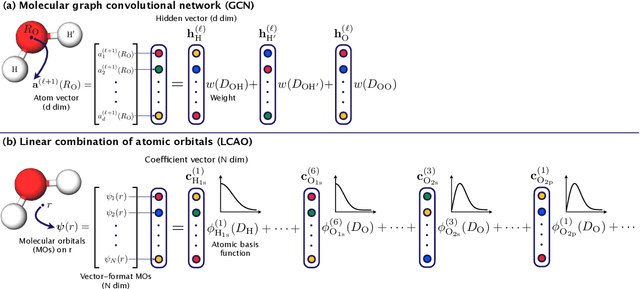
On the equivalence of molecular graph convolution and molecular wave function with poor basis set

In this study, we demonstrate that the linear combination of atomic orbitals (LCAO), an approximation of quantum physics introduced by Pauling and Lennard-Jones in the 1920s, corresponds to graph convolutional networks (GCNs) for molecules. However, GCNs involve unnecessary nonlinearity and deep architecture. We also verify that molecular GCNs are based on a poor basis function set compared with the standard one used in theoretical calculations or quantum chemical simulations. From these observations, we describe the quantum deep field (QDF), a machine learning (ML) model based on an underlying quantum physics, in particular the density functional theory (DFT). We believe that the QDF model can be easily understood because it can be regarded as a single linear layer GCN. Moreover, it uses two vanilla feedforward neural networks to learn an energy functional and a Hohenberg--Kohn map that have nonlinearities inherent in quantum physics and the DFT. For molecular energy prediction tasks, we demonstrated the viability of an ``extrapolation,'' in which we trained a QDF model with small molecules, tested it with large molecules, and achieved high extrapolation performance. This will lead to reliable and practical applications for discovering effective materials. The implementation is available at https://github.com/masashitsubaki/QuantumDeepField_molecule.

Quantum deep field: data-driven wave function, electron density generation, and atomization energy prediction and extrapolation with machine learning

Deep neural networks (DNNs) have been used to successfully predict molecular properties calculated based on the Kohn--Sham density functional theory (KS-DFT). Although this prediction is fast and accurate, we believe that a DNN model for KS-DFT must not only predict the properties but also provide the electron density of a molecule. This letter presents the quantum deep field (QDF), which provides the electron density with an unsupervised but end-to-end physics-informed modeling by learning the atomization energy on a large-scale dataset. QDF performed well at atomization energy prediction, generated valid electron density, and demonstrated extrapolation. Our QDF implementation is available at https://github.com/masashitsubaki/QuantumDeepField_molecule.

Mean-field theory of graph neural networks in graph partitioning

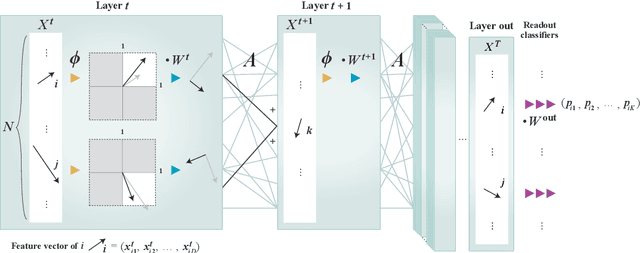
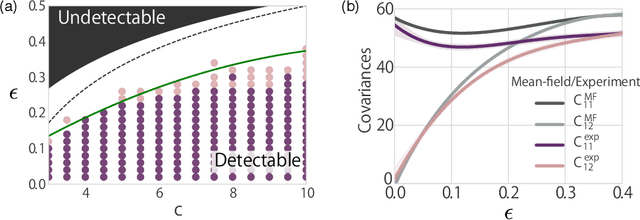
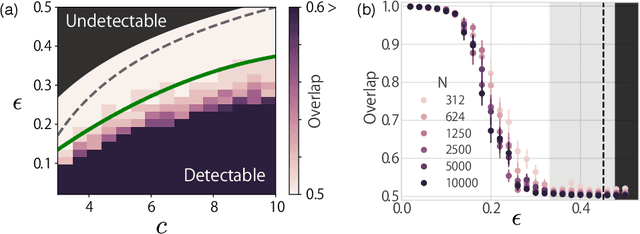
A theoretical performance analysis of the graph neural network (GNN) is presented. For classification tasks, the neural network approach has the advantage in terms of flexibility that it can be employed in a data-driven manner, whereas Bayesian inference requires the assumption of a specific model. A fundamental question is then whether GNN has a high accuracy in addition to this flexibility. Moreover, whether the achieved performance is predominately a result of the backpropagation or the architecture itself is a matter of considerable interest. To gain a better insight into these questions, a mean-field theory of a minimal GNN architecture is developed for the graph partitioning problem. This demonstrates a good agreement with numerical experiments.