Why Physics Still Matters: Improving Machine Learning Prediction of Material Properties with Phonon-Informed Datasets

Machine learning (ML) methods have become powerful tools for predicting material properties with near first-principles accuracy and vastly reduced computational cost. However, the performance of ML models critically depends on the quality, size, and diversity of the training dataset. In materials science, this dependence is particularly important for learning from low-symmetry atomistic configurations that capture thermal excitations, structural defects, and chemical disorder, features that are ubiquitous in real materials but underrepresented in most datasets. The absence of systematic strategies for generating representative training data may therefore limit the predictive power of ML models in technologically critical fields such as energy conversion and photonics. In this work, we assess the effectiveness of graph neural network (GNN) models trained on two fundamentally different types of datasets: one composed of randomly generated atomic configurations and another constructed using physically informed sampling based on lattice vibrations. As a case study, we address the challenging task of predicting electronic and mechanical properties of a prototypical family of optoelectronic materials under realistic finite-temperature conditions. We find that the phonons-informed model consistently outperforms the randomly trained counterpart, despite relying on fewer data points. Explainability analyses further reveal that high-performing models assign greater weight to chemically meaningful bonds that control property variations, underscoring the importance of physically guided data generation. Overall, this work demonstrates that larger datasets do not necessarily yield better GNN predictive models and introduces a simple and general strategy for efficiently constructing high-quality training data in materials informatics.

Generative Inverse Design of Crystal Structures via Diffusion Models with Transformers

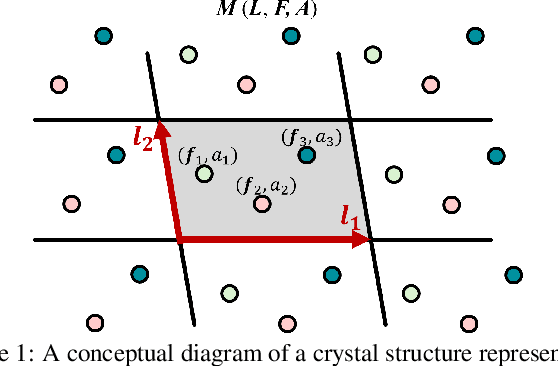
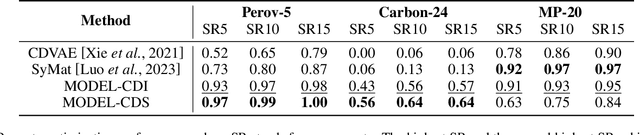
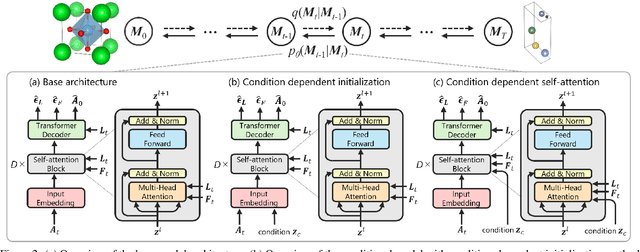
Recent advances in deep learning have enabled the generation of realistic data by training generative models on large datasets of text, images, and audio. While these models have demonstrated exceptional performance in generating novel and plausible data, it remains an open question whether they can effectively accelerate scientific discovery through the data generation and drive significant advancements across various scientific fields. In particular, the discovery of new inorganic materials with promising properties poses a critical challenge, both scientifically and for industrial applications. However, unlike textual or image data, materials, or more specifically crystal structures, consist of multiple types of variables - including lattice vectors, atom positions, and atomic species. This complexity in data give rise to a variety of approaches for representing and generating such data. Consequently, the design choices of generative models for crystal structures remain an open question. In this study, we explore a new type of diffusion model for the generative inverse design of crystal structures, with a backbone based on a Transformer architecture. We demonstrate our models are superior to previous methods in their versatility for generating crystal structures with desired properties. Furthermore, our empirical results suggest that the optimal conditioning methods vary depending on the dataset.

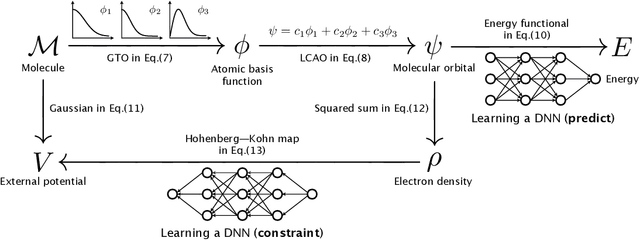
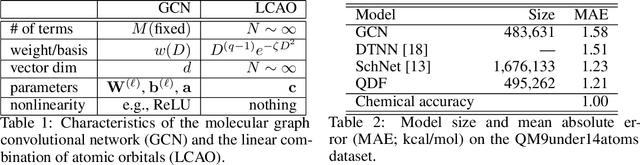
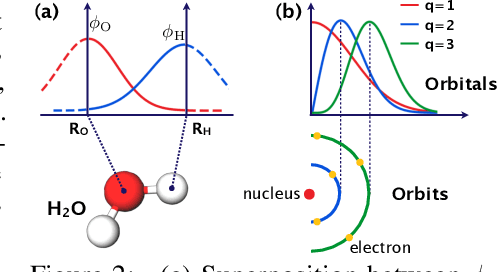
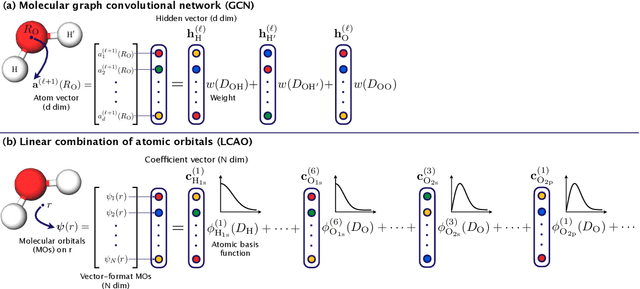
On the equivalence of molecular graph convolution and molecular wave function with poor basis set

In this study, we demonstrate that the linear combination of atomic orbitals (LCAO), an approximation of quantum physics introduced by Pauling and Lennard-Jones in the 1920s, corresponds to graph convolutional networks (GCNs) for molecules. However, GCNs involve unnecessary nonlinearity and deep architecture. We also verify that molecular GCNs are based on a poor basis function set compared with the standard one used in theoretical calculations or quantum chemical simulations. From these observations, we describe the quantum deep field (QDF), a machine learning (ML) model based on an underlying quantum physics, in particular the density functional theory (DFT). We believe that the QDF model can be easily understood because it can be regarded as a single linear layer GCN. Moreover, it uses two vanilla feedforward neural networks to learn an energy functional and a Hohenberg--Kohn map that have nonlinearities inherent in quantum physics and the DFT. For molecular energy prediction tasks, we demonstrated the viability of an ``extrapolation,'' in which we trained a QDF model with small molecules, tested it with large molecules, and achieved high extrapolation performance. This will lead to reliable and practical applications for discovering effective materials. The implementation is available at https://github.com/masashitsubaki/QuantumDeepField_molecule.

Quantum deep field: data-driven wave function, electron density generation, and atomization energy prediction and extrapolation with machine learning

Deep neural networks (DNNs) have been used to successfully predict molecular properties calculated based on the Kohn--Sham density functional theory (KS-DFT). Although this prediction is fast and accurate, we believe that a DNN model for KS-DFT must not only predict the properties but also provide the electron density of a molecule. This letter presents the quantum deep field (QDF), which provides the electron density with an unsupervised but end-to-end physics-informed modeling by learning the atomization energy on a large-scale dataset. QDF performed well at atomization energy prediction, generated valid electron density, and demonstrated extrapolation. Our QDF implementation is available at https://github.com/masashitsubaki/QuantumDeepField_molecule.