Delta-Closure Structure for Studying Data Distribution

In this paper, we revisit pattern mining and study the distribution underlying a binary dataset thanks to the closure structure which is based on passkeys, i.e., minimum generators in equivalence classes robust to noise. We introduce $\Delta$-closedness, a generalization of the closure operator, where $\Delta$ measures how a closed set differs from its upper neighbors in the partial order induced by closure. A $\Delta$-class of equivalence includes minimum and maximum elements and allows us to characterize the distribution underlying the data. Moreover, the set of $\Delta$-classes of equivalence can be partitioned into the so-called $\Delta$-closure structure. In particular, a $\Delta$-class of equivalence with a high level demonstrates correlations among many attributes, which are supported by more observations when $\Delta$ is large. In the experiments, we study the $\Delta$-closure structure of several real-world datasets and show that this structure is very stable for large $\Delta$ and does not substantially depend on the data sampling used for the analysis.

Mint: MDL-based approach for Mining INTeresting Numerical Pattern Sets

Pattern mining is well established in data mining research, especially for mining binary datasets. Surprisingly, there is much less work about numerical pattern mining and this research area remains under-explored. In this paper, we propose Mint, an efficient MDL-based algorithm for mining numerical datasets. The MDL principle is a robust and reliable framework widely used in pattern mining, and as well in subgroup discovery. In Mint we reuse MDL for discovering useful patterns and returning a set of non-redundant overlapping patterns with well-defined boundaries and covering meaningful groups of objects. Mint is not alone in the category of numerical pattern miners based on MDL. In the experiments presented in the paper we show that Mint outperforms competitors among which Slim and RealKrimp.

Discovery data topology with the closure structure. Theoretical and practical aspects

In this paper, we are revisiting pattern mining and especially itemset mining, which allows one to analyze binary datasets in searching for interesting and meaningful association rules and respective itemsets in an unsupervised way. While a summarization of a dataset based on a set of patterns does not provide a general and satisfying view over a dataset, we introduce a concise representation --the closure structure-- based on closed itemsets and their minimum generators, for capturing the intrinsic content of a dataset. The closure structure allows one to understand the topology of the dataset in the whole and the inherent complexity of the data. We propose a formalization of the closure structure in terms of Formal Concept Analysis, which is well adapted to study this data topology. We present and demonstrate theoretical results, and as well, practical results using the GDPM algorithm. GDPM is rather unique in its functionality as it returns a characterization of the topology of a dataset in terms of complexity levels, highlighting the diversity and the distribution of the itemsets. Finally, a series of experiments shows how GDPM can be practically used and what can be expected from the output.

From-Below Boolean Matrix Factorization Algorithm Based on MDL

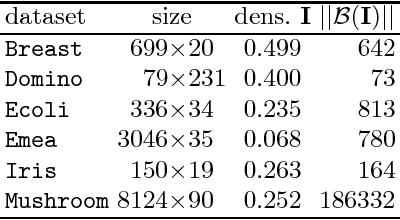
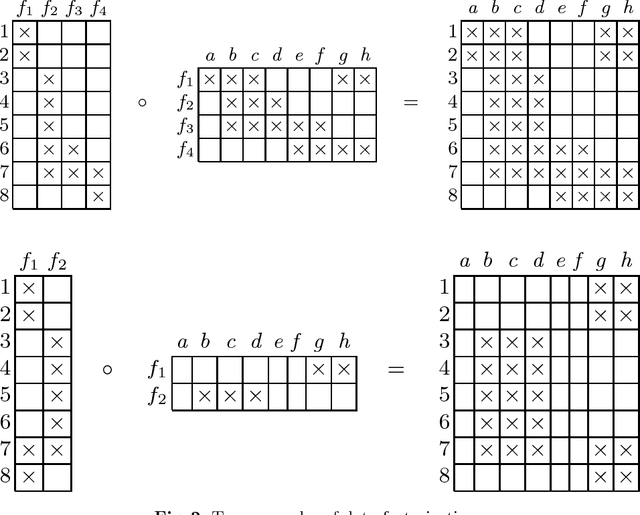
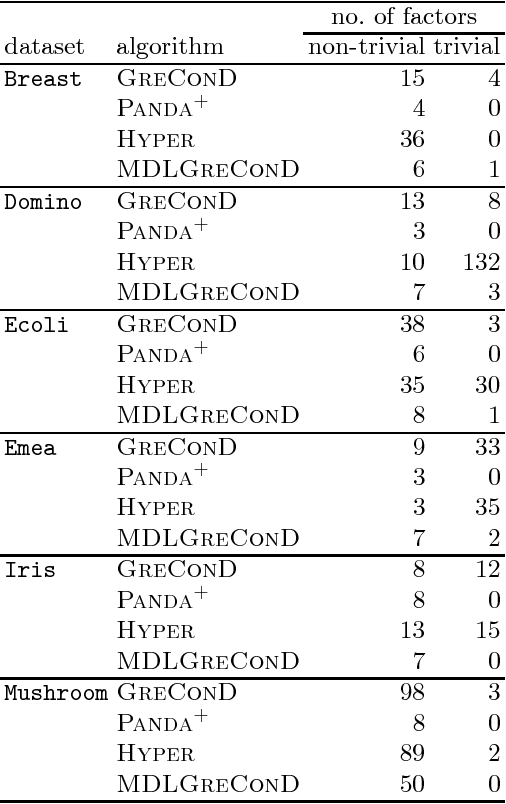
During the past few years Boolean matrix factorization (BMF) has become an important direction in data analysis. The minimum description length principle (MDL) was successfully adapted in BMF for the model order selection. Nevertheless, a BMF algorithm performing good results from the standpoint of standard measures in BMF is missing. In this paper, we propose a novel from-below Boolean matrix factorization algorithm based on formal concept analysis. The algorithm utilizes the MDL principle as a criterion for the factor selection. On various experiments we show that the proposed algorithm outperforms---from different standpoints---existing state-of-the-art BMF algorithms.

On interestingness measures of formal concepts

Formal concepts and closed itemsets proved to be of big importance for knowledge discovery, both as a tool for concise representation of association rules and a tool for clustering and constructing domain taxonomies and ontologies. Exponential explosion makes it difficult to consider the whole concept lattice arising from data, one needs to select most useful and interesting concepts. In this paper interestingness measures of concepts are considered and compared with respect to various aspects, such as efficiency of computation and applicability to noisy data and performing ranking correlation.