Aleksey Buzmakov
Delta-Closure Structure for Studying Data Distribution
Oct 13, 2022



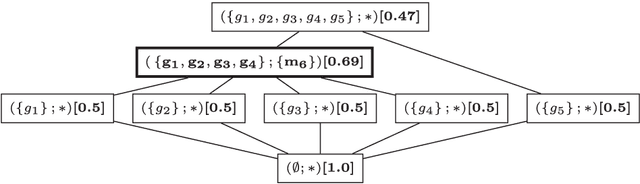
Abstract:In this paper, we revisit pattern mining and study the distribution underlying a binary dataset thanks to the closure structure which is based on passkeys, i.e., minimum generators in equivalence classes robust to noise. We introduce $\Delta$-closedness, a generalization of the closure operator, where $\Delta$ measures how a closed set differs from its upper neighbors in the partial order induced by closure. A $\Delta$-class of equivalence includes minimum and maximum elements and allows us to characterize the distribution underlying the data. Moreover, the set of $\Delta$-classes of equivalence can be partitioned into the so-called $\Delta$-closure structure. In particular, a $\Delta$-class of equivalence with a high level demonstrates correlations among many attributes, which are supported by more observations when $\Delta$ is large. In the experiments, we study the $\Delta$-closure structure of several real-world datasets and show that this structure is very stable for large $\Delta$ and does not substantially depend on the data sampling used for the analysis.
The Comparison of Methods for Individual Treatment Effect Detection
Dec 03, 2019

Abstract:Today, treatment effect estimation at the individual level is a vital problem in many areas of science and business. For example, in marketing, estimates of the treatment effect are used to select the most efficient promo-mechanics; in medicine, individual treatment effects are used to determine the optimal dose of medication for each patient and so on. At the same time, the question on choosing the best method, i.e., the method that ensures the smallest predictive error (for instance, RMSE) or the highest total (average) value of the effect, remains open. Accordingly, in this paper we compare the effectiveness of machine learning methods for estimation of individual treatment effects. The comparison is performed on the Criteo Uplift Modeling Dataset. In this paper we show that the combination of the Logistic Regression method and the Difference Score method as well as Uplift Random Forest method provide the best correctness of Individual Treatment Effect prediction on the top 30\% observations of the test dataset.
Machine learning for subgroup discovery under treatment effect
Feb 27, 2019Abstract:In many practical tasks it is needed to estimate an effect of treatment on individual level. For example, in medicine it is essential to determine the patients that would benefit from a certain medicament. In marketing, knowing the persons that are likely to buy a new product would reduce the amount of spam. In this chapter, we review the methods to estimate an individual treatment effect from a randomized trial, i.e., an experiment when a part of individuals receives a new treatment, while the others do not. Finally, it is shown that new efficient methods are needed in this domain.
Mining Best Closed Itemsets for Projection-antimonotonic Constraints in Polynomial Time
Mar 28, 2017



Abstract:The exponential explosion of the set of patterns is one of the main challenges in pattern mining. This challenge is approached by introducing a constraint for pattern selection. One of the first constraints proposed in pattern mining is support (frequency) of a pattern in a dataset. Frequency is an anti-monotonic function, i.e., given an infrequent pattern, all its superpatterns are not frequent. However, many other constraints for pattern selection are neither monotonic nor anti-monotonic, which makes it difficult to generate patterns satisfying these constraints. In order to deal with nonmonotonic constraints we introduce the notion of "projection antimonotonicity" and SOFIA algorithm that allow generating best patterns for a class of nonmonotonic constraints. Cosine interest, robustness, stability of closed itemsets, and the associated delta-measure are among these constraints. SOFIA starts from light descriptions of transactions in dataset (a small set of items in the case of itemset description) and then iteratively adds more information to these descriptions (more items with indication of tidsets they describe).
Fast Generation of Best Interval Patterns for Nonmonotonic Constraints
Jun 16, 2015



Abstract:In pattern mining, the main challenge is the exponential explosion of the set of patterns. Typically, to solve this problem, a constraint for pattern selection is introduced. One of the first constraints proposed in pattern mining is support (frequency) of a pattern in a dataset. Frequency is an anti-monotonic function, i.e., given an infrequent pattern, all its superpatterns are not frequent. However, many other constraints for pattern selection are not (anti-)monotonic, which makes it difficult to generate patterns satisfying these constraints. In this paper we introduce the notion of projection-antimonotonicity and $\theta$-$\Sigma\o\phi\iota\alpha$ algorithm that allows efficient generation of the best patterns for some nonmonotonic constraints. In this paper we consider stability and $\Delta$-measure, which are nonmonotonic constraints, and apply them to interval tuple datasets. In the experiments, we compute best interval tuple patterns w.r.t. these measures and show the advantage of our approach over postfiltering approaches. KEYWORDS: Pattern mining, nonmonotonic constraints, interval tuple data
On mining complex sequential data by means of FCA and pattern structures
Apr 09, 2015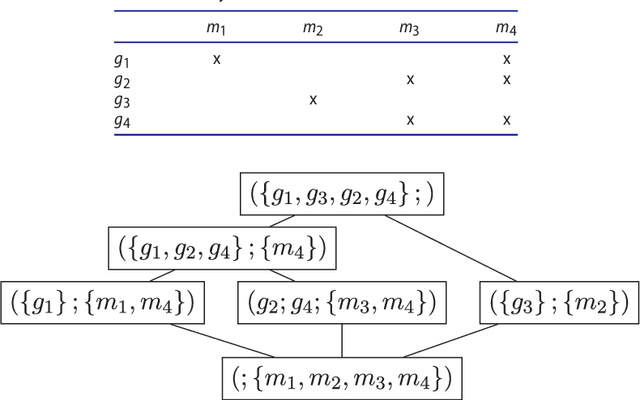


Abstract:Nowadays data sets are available in very complex and heterogeneous ways. Mining of such data collections is essential to support many real-world applications ranging from healthcare to marketing. In this work, we focus on the analysis of "complex" sequential data by means of interesting sequential patterns. We approach the problem using the elegant mathematical framework of Formal Concept Analysis (FCA) and its extension based on "pattern structures". Pattern structures are used for mining complex data (such as sequences or graphs) and are based on a subsumption operation, which in our case is defined with respect to the partial order on sequences. We show how pattern structures along with projections (i.e., a data reduction of sequential structures), are able to enumerate more meaningful patterns and increase the computing efficiency of the approach. Finally, we show the applicability of the presented method for discovering and analyzing interesting patient patterns from a French healthcare data set on cancer. The quantitative and qualitative results (with annotations and analysis from a physician) are reported in this use case which is the main motivation for this work. Keywords: data mining; formal concept analysis; pattern structures; projections; sequences; sequential data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge