From-Below Boolean Matrix Factorization Algorithm Based on MDL

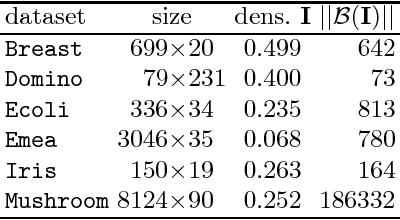
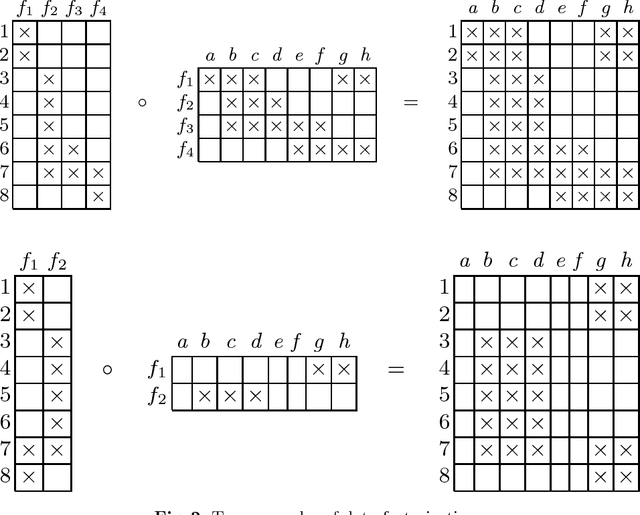
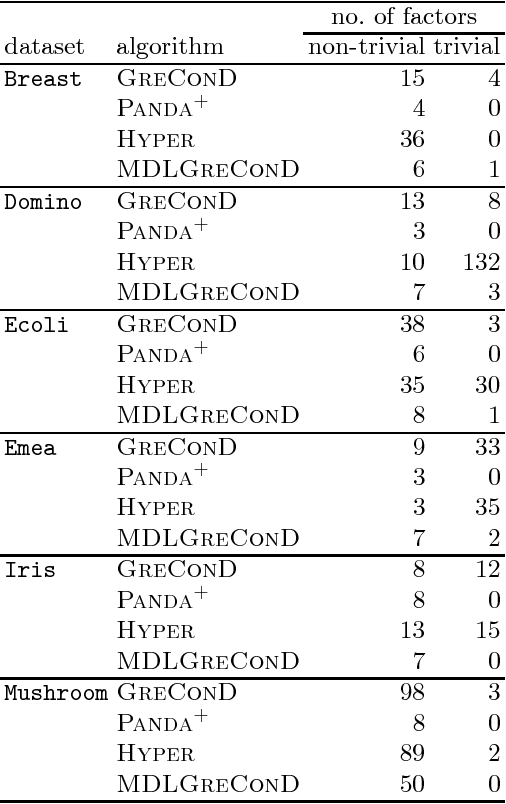
During the past few years Boolean matrix factorization (BMF) has become an important direction in data analysis. The minimum description length principle (MDL) was successfully adapted in BMF for the model order selection. Nevertheless, a BMF algorithm performing good results from the standpoint of standard measures in BMF is missing. In this paper, we propose a novel from-below Boolean matrix factorization algorithm based on formal concept analysis. The algorithm utilizes the MDL principle as a criterion for the factor selection. On various experiments we show that the proposed algorithm outperforms---from different standpoints---existing state-of-the-art BMF algorithms.

From-Below Approximations in Boolean Matrix Factorization: Geometry and New Algorithm

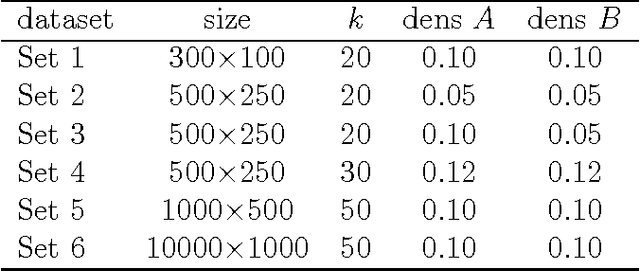
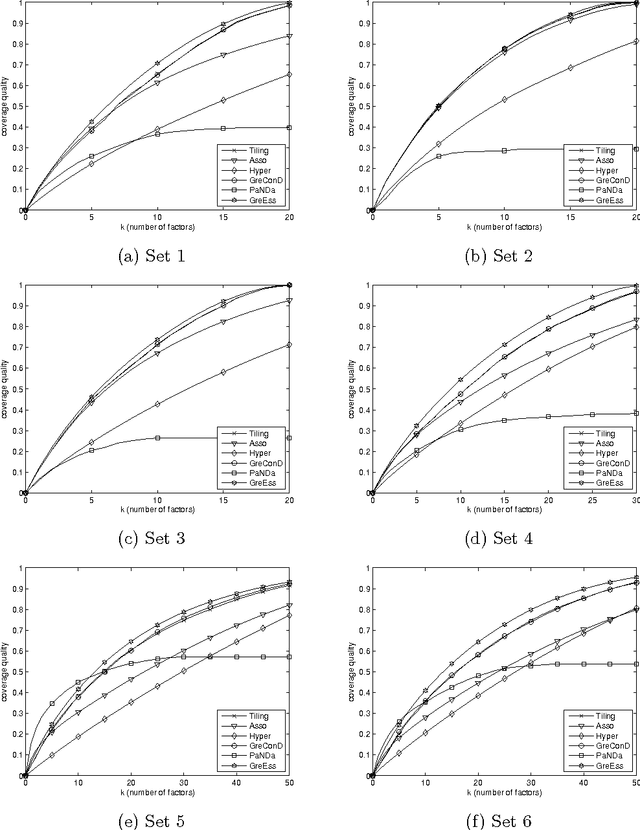
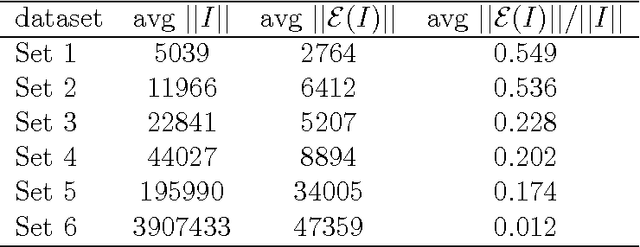
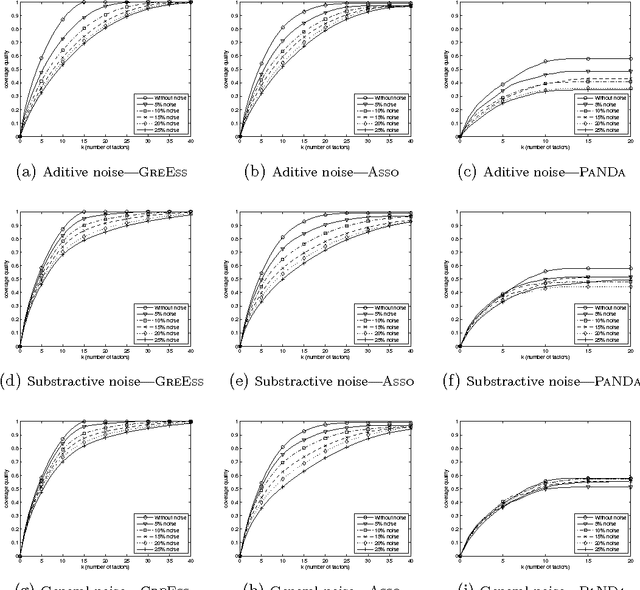
We present new results on Boolean matrix factorization and a new algorithm based on these results. The results emphasize the significance of factorizations that provide from-below approximations of the input matrix. While the previously proposed algorithms do not consider the possibly different significance of different matrix entries, our results help measure such significance and suggest where to focus when computing factors. An experimental evaluation of the new algorithm on both synthetic and real data demonstrates its good performance in terms of good coverage by the first k factors as well as a small number of factors needed for exact decomposition and indicates that the algorithm outperforms the available ones in these terms. We also propose future research topics.