From-Below Approximations in Boolean Matrix Factorization: Geometry and New Algorithm

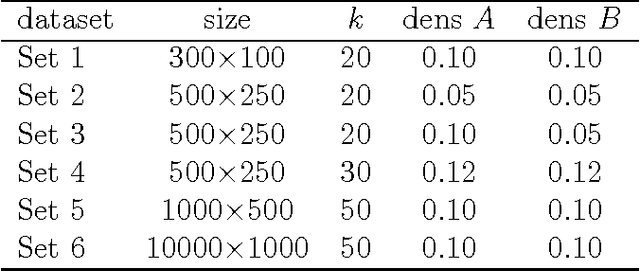
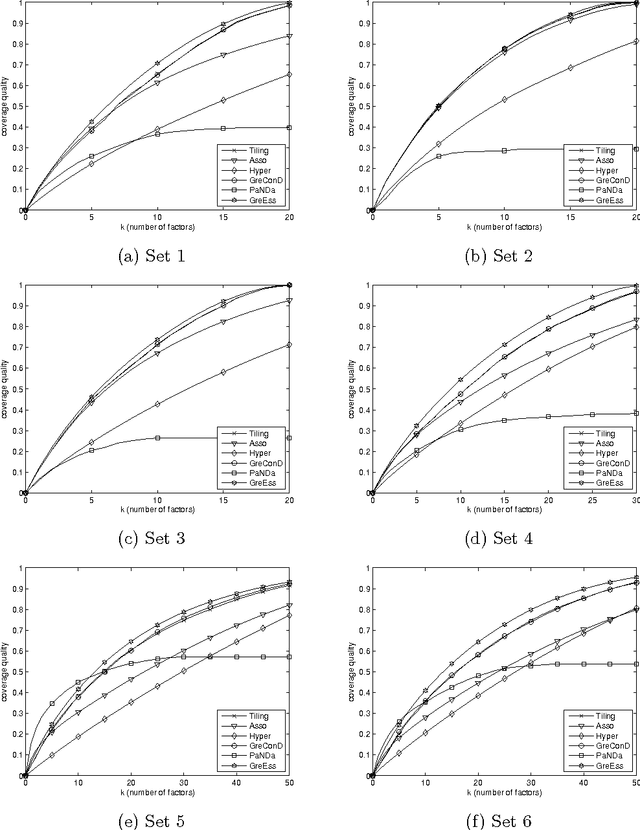
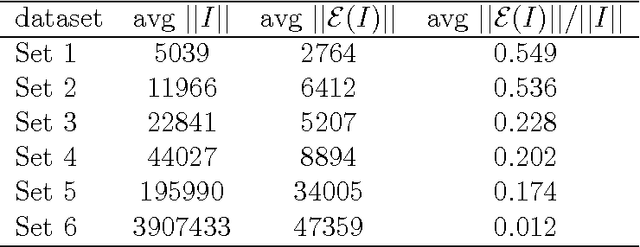
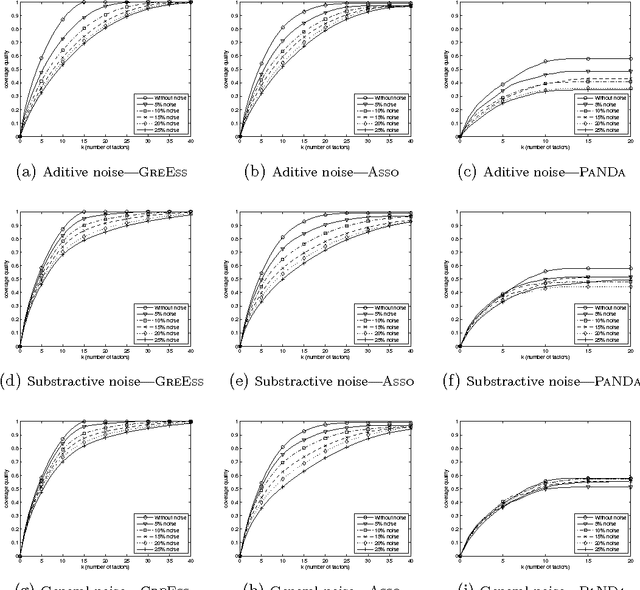
We present new results on Boolean matrix factorization and a new algorithm based on these results. The results emphasize the significance of factorizations that provide from-below approximations of the input matrix. While the previously proposed algorithms do not consider the possibly different significance of different matrix entries, our results help measure such significance and suggest where to focus when computing factors. An experimental evaluation of the new algorithm on both synthetic and real data demonstrates its good performance in terms of good coverage by the first k factors as well as a small number of factors needed for exact decomposition and indicates that the algorithm outperforms the available ones in these terms. We also propose future research topics.

Discovery of factors in matrices with grades

We present an approach to decomposition and factor analysis of matrices with ordinal data. The matrix entries are grades to which objects represented by rows satisfy attributes represented by columns, e.g. grades to which an image is red, a product has a given feature, or a person performs well in a test. We assume that the grades form a bounded scale equipped with certain aggregation operators and conforms to the structure of a complete residuated lattice. We present a greedy approximation algorithm for the problem of decomposition of such matrix in a product of two matrices with grades under the restriction that the number of factors be small. Our algorithm is based on a geometric insight provided by a theorem identifying particular rectangular-shaped submatrices as optimal factors for the decompositions. These factors correspond to formal concepts of the input data and allow an easy interpretation of the decomposition. We present illustrative examples and experimental evaluation.