Computing sets of graded attribute implications with witnessed non-redundancy

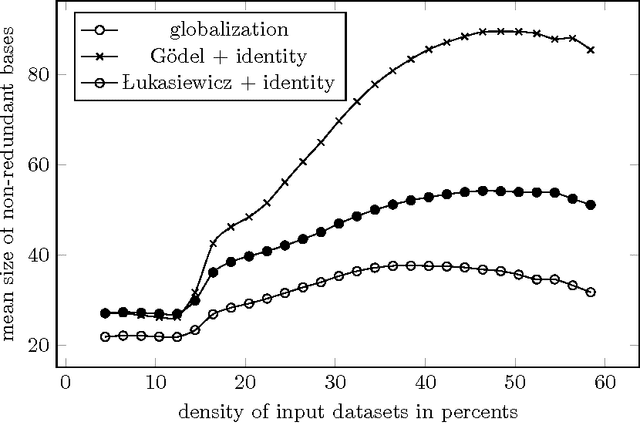
In this paper we extend our previous results on sets of graded attribute implications with witnessed non-redundancy. We assume finite residuated lattices as structures of truth degrees and use arbitrary idempotent truth-stressing linguistic hedges as parameters which influence the semantics of graded attribute implications. In this setting, we introduce algorithm which transforms any set of graded attribute implications into an equivalent non-redundant set of graded attribute implications with saturated consequents whose non-redundancy is witnessed by antecedents of the formulas. As a consequence, we solve the open problem regarding the existence of general systems of pseudo-intents which appear in formal concept analysis of object-attribute data with graded attributes and linguistic hedges. Furthermore, we show a polynomial-time procedure for determining bases given by general systems of pseudo-intents from sets of graded attribute implications which are complete in data.

On sets of graded attribute implications with witnessed non-redundancy

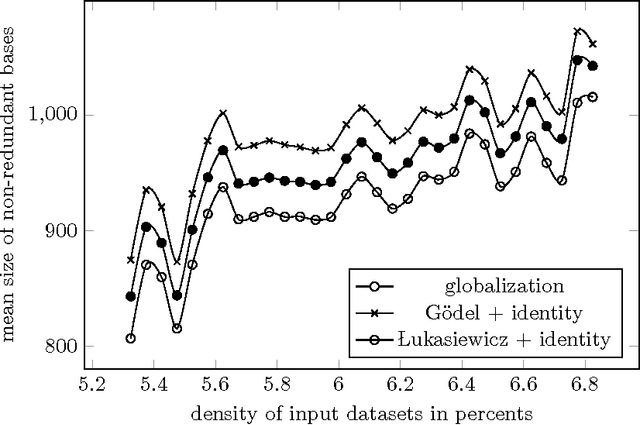
We study properties of particular non-redundant sets of if-then rules describing dependencies between graded attributes. We introduce notions of saturation and witnessed non-redundancy of sets of graded attribute implications are show that bases of graded attribute implications given by systems of pseudo-intents correspond to non-redundant sets of graded attribute implications with saturated consequents where the non-redundancy is witnessed by antecedents of the contained graded attribute implications. We introduce an algorithm which transforms any complete set of graded attribute implications parameterized by globalization into a base given by pseudo-intents. Experimental evaluation is provided to compare the method of obtaining bases for general parameterizations by hedges with earlier graph-based approaches.

Logic of temporal attribute implications

We study logic for reasoning with if-then formulas describing dependencies between attributes of objects which are observed in consecutive points in time. We introduce semantic entailment of the formulas, show its fixed-point characterization, investigate closure properties of model classes, present an axiomatization and prove its completeness, and investigate alternative axiomatizations and normalized proofs. We investigate decidability and complexity issues of the logic and prove that the entailment problem is NP-hard and belongs to EXPSPACE. We show that by restricting to predictive formulas, the entailment problem is decidable in pseudo-linear time.

Fuzzy inequational logic

We present a logic for reasoning about graded inequalities which generalizes the ordinary inequational logic used in universal algebra. The logic deals with atomic predicate formulas of the form of inequalities between terms and formalizes their semantic entailment and provability in graded setting which allows to draw partially true conclusions from partially true assumptions. We follow the Pavelka approach and define general degrees of semantic entailment and provability using complete residuated lattices as structures of truth degrees. We prove the logic is Pavelka-style complete. Furthermore, we present a logic for reasoning about graded if-then rules which is obtained as particular case of the general result.

Parameterizing the semantics of fuzzy attribute implications by systems of isotone Galois connections

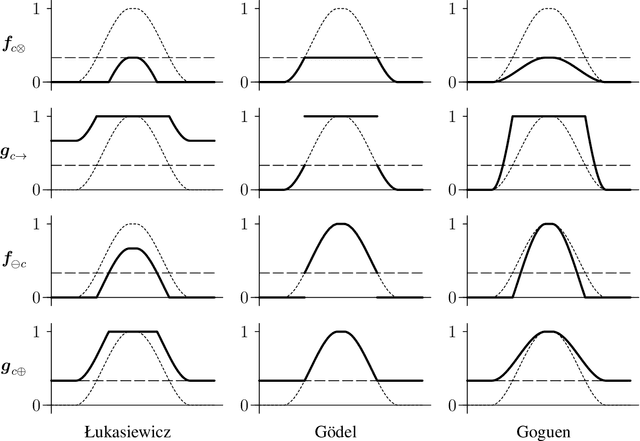
We study the semantics of fuzzy if-then rules called fuzzy attribute implications parameterized by systems of isotone Galois connections. The rules express dependencies between fuzzy attributes in object-attribute incidence data. The proposed parameterizations are general and include as special cases the parameterizations by linguistic hedges used in earlier approaches. We formalize the general parameterizations, propose bivalent and graded notions of semantic entailment of fuzzy attribute implications, show their characterization in terms of least models and complete axiomatization, and provide characterization of bases of fuzzy attribute implications derived from data.

On minimal sets of graded attribute implications

We explore the structure of non-redundant and minimal sets consisting of graded if-then rules. The rules serve as graded attribute implications in object-attribute incidence data and as similarity-based functional dependencies in a similarity-based generalization of the relational model of data. Based on our observations, we derive a polynomial-time algorithm which transforms a given finite set of rules into an equivalent one which has the least size in terms of the number of rules.

Discovery of factors in matrices with grades

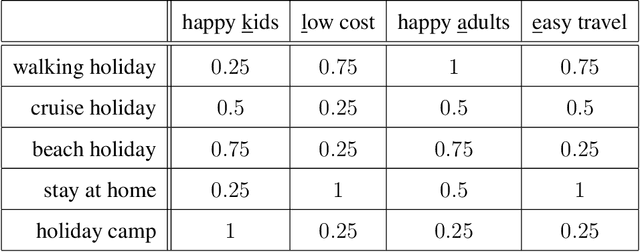
We present an approach to decomposition and factor analysis of matrices with ordinal data. The matrix entries are grades to which objects represented by rows satisfy attributes represented by columns, e.g. grades to which an image is red, a product has a given feature, or a person performs well in a test. We assume that the grades form a bounded scale equipped with certain aggregation operators and conforms to the structure of a complete residuated lattice. We present a greedy approximation algorithm for the problem of decomposition of such matrix in a product of two matrices with grades under the restriction that the number of factors be small. Our algorithm is based on a geometric insight provided by a theorem identifying particular rectangular-shaped submatrices as optimal factors for the decompositions. These factors correspond to formal concepts of the input data and allow an easy interpretation of the decomposition. We present illustrative examples and experimental evaluation.