Computing sets of graded attribute implications with witnessed non-redundancy
Paper and Code
Nov 05, 2015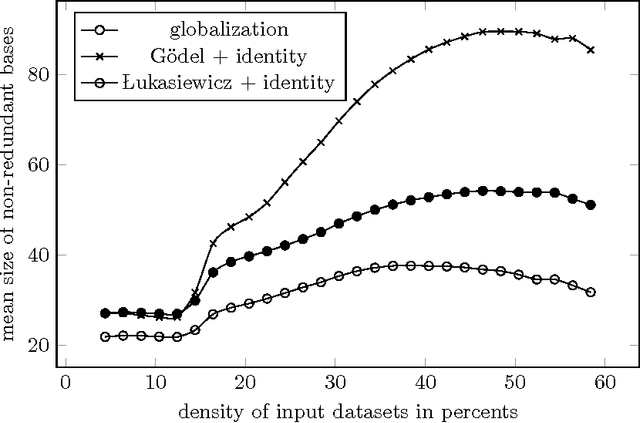
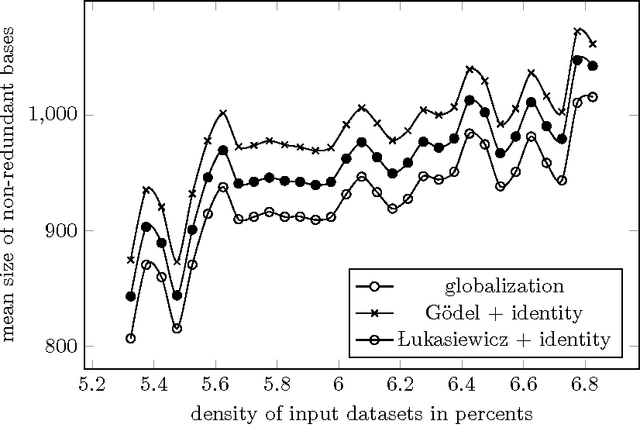
In this paper we extend our previous results on sets of graded attribute implications with witnessed non-redundancy. We assume finite residuated lattices as structures of truth degrees and use arbitrary idempotent truth-stressing linguistic hedges as parameters which influence the semantics of graded attribute implications. In this setting, we introduce algorithm which transforms any set of graded attribute implications into an equivalent non-redundant set of graded attribute implications with saturated consequents whose non-redundancy is witnessed by antecedents of the formulas. As a consequence, we solve the open problem regarding the existence of general systems of pseudo-intents which appear in formal concept analysis of object-attribute data with graded attributes and linguistic hedges. Furthermore, we show a polynomial-time procedure for determining bases given by general systems of pseudo-intents from sets of graded attribute implications which are complete in data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge