Estimating Causal Effects in Partially Directed Parametric Causal Factor Graphs

Lifting uses a representative of indistinguishable individuals to exploit symmetries in probabilistic relational models, denoted as parametric factor graphs, to speed up inference while maintaining exact answers. In this paper, we show how lifting can be applied to causal inference in partially directed graphs, i.e., graphs that contain both directed and undirected edges to represent causal relationships between random variables. We present partially directed parametric causal factor graphs (PPCFGs) as a generalisation of previously introduced parametric causal factor graphs, which require a fully directed graph. We further show how causal inference can be performed on a lifted level in PPCFGs, thereby extending the applicability of lifted causal inference to a broader range of models requiring less prior knowledge about causal relationships.

Lifted Causal Inference in Relational Domains

Lifted inference exploits symmetries in probabilistic graphical models by using a representative for indistinguishable objects, thereby speeding up query answering while maintaining exact answers. Even though lifting is a well-established technique for the task of probabilistic inference in relational domains, it has not yet been applied to the task of causal inference. In this paper, we show how lifting can be applied to efficiently compute causal effects in relational domains. More specifically, we introduce parametric causal factor graphs as an extension of parametric factor graphs incorporating causal knowledge and give a formal semantics of interventions therein. We further present the lifted causal inference algorithm to compute causal effects on a lifted level, thereby drastically speeding up causal inference compared to propositional inference, e.g., in causal Bayesian networks. In our empirical evaluation, we demonstrate the effectiveness of our approach.

Colour Passing Revisited: Lifted Model Construction with Commutative Factors

Lifted probabilistic inference exploits symmetries in a probabilistic model to allow for tractable probabilistic inference with respect to domain sizes. To apply lifted inference, a lifted representation has to be obtained, and to do so, the so-called colour passing algorithm is the state of the art. The colour passing algorithm, however, is bound to a specific inference algorithm and we found that it ignores commutativity of factors while constructing a lifted representation. We contribute a modified version of the colour passing algorithm that uses logical variables to construct a lifted representation independent of a specific inference algorithm while at the same time exploiting commutativity of factors during an offline-step. Our proposed algorithm efficiently detects more symmetries than the state of the art and thereby drastically increases compression, yielding significantly faster online query times for probabilistic inference when the resulting model is applied.

DPM: Clustering Sensitive Data through Separation

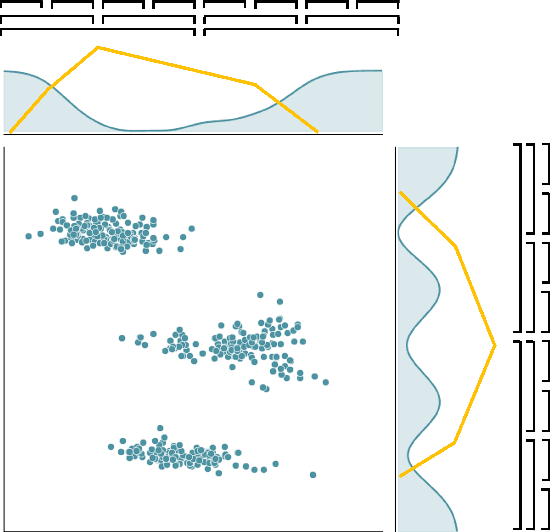
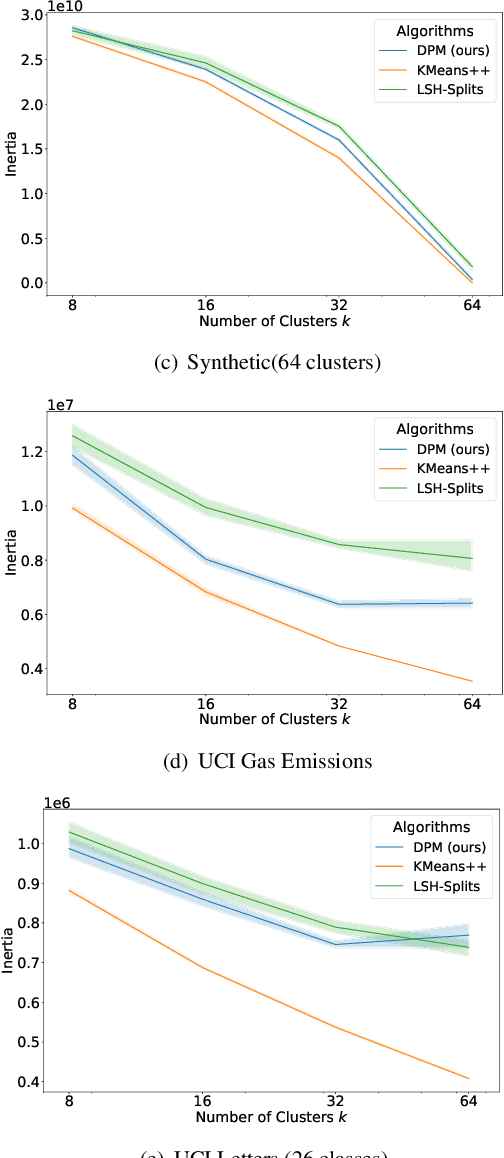
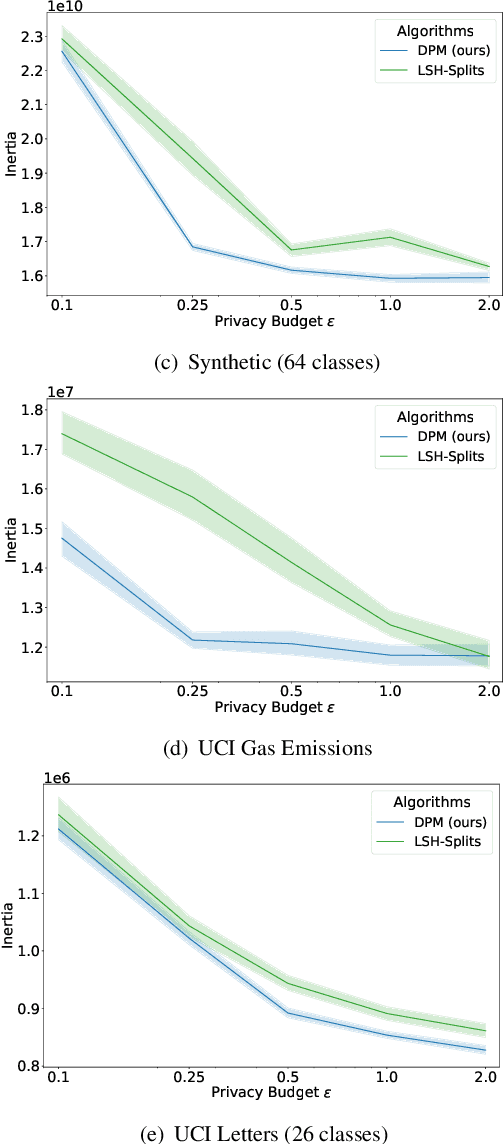
Privacy-preserving clustering groups data points in an unsupervised manner whilst ensuring that sensitive information remains protected. Previous privacy-preserving clustering focused on identifying concentration of point clouds. In this paper, we take another path and focus on identifying appropriate separators that split a data set. We introduce the novel differentially private clustering algorithm DPM that searches for accurate data point separators in a differentially private manner. DPM addresses two key challenges for finding accurate separators: identifying separators that are large gaps between clusters instead of small gaps within a cluster and, to efficiently spend the privacy budget, prioritising separators that split the data into large subparts. Using the differentially private Exponential Mechanism, DPM randomly chooses cluster separators with provably high utility: For a data set $D$, if there is a wide low-density separator in the central $60\%$ quantile, DPM finds that separator with probability $1 - \exp(-\sqrt{|D|})$. Our experimental evaluation demonstrates that DPM achieves significant improvements in terms of the clustering metric inertia. With the inertia results of the non-private KMeans++ as a baseline, for $\varepsilon = 1$ and $\delta=10^{-5}$ DPM improves upon the difference to the baseline by up to $50\%$ for a synthetic data set and by up to $62\%$ for a real-world data set compared to a state-of-the-art clustering algorithm by Chang and Kamath.

Lifting DecPOMDPs for Nanoscale Systems -- A Work in Progress

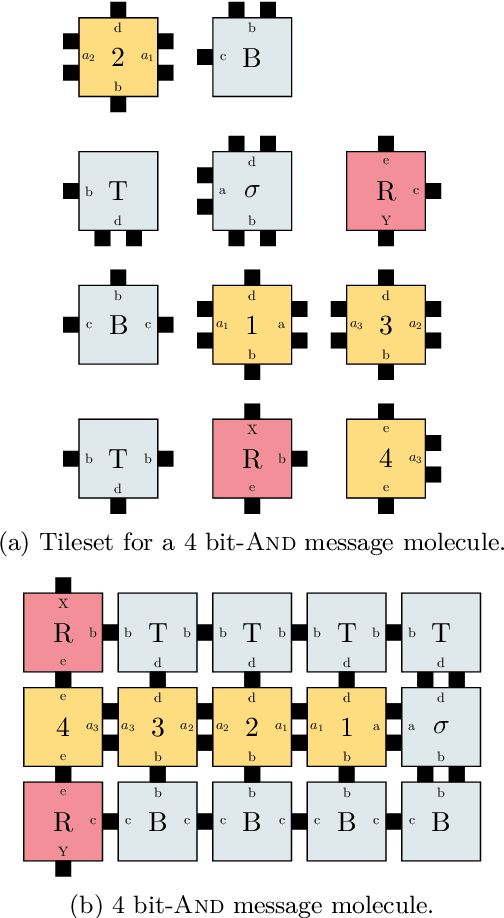
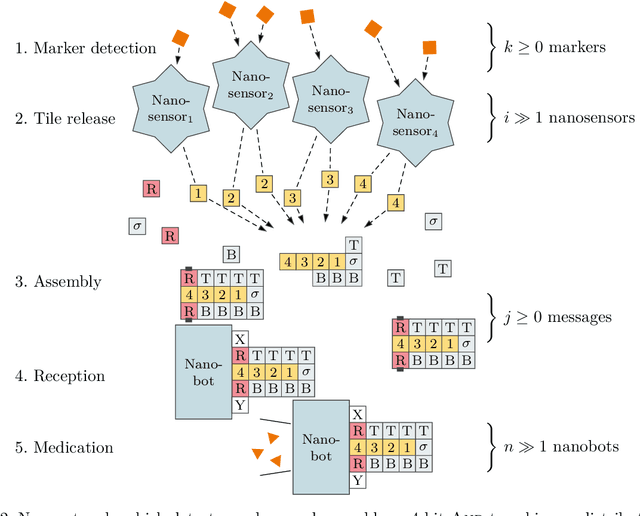
DNA-based nanonetworks have a wide range of promising use cases, especially in the field of medicine. With a large set of agents, a partially observable stochastic environment, and noisy observations, such nanoscale systems can be modelled as a decentralised, partially observable, Markov decision process (DecPOMDP). As the agent set is a dominating factor, this paper presents (i) lifted DecPOMDPs, partitioning the agent set into sets of indistinguishable agents, reducing the worst-case space required, and (ii) a nanoscale medical system as an application. Future work turns to solving and implementing lifted DecPOMDPs.

Exploring Unknown Universes in Probabilistic Relational Models

Large probabilistic models are often shaped by a pool of known individuals (a universe) and relations between them. Lifted inference algorithms handle sets of known individuals for tractable inference. Universes may not always be known, though, or may only described by assumptions such as "small universes are more likely". Without a universe, inference is no longer possible for lifted algorithms, losing their advantage of tractable inference. The aim of this paper is to define a semantics for models with unknown universes decoupled from a specific constraint language to enable lifted and thereby, tractable inference.

Taming Reasoning in Temporal Probabilistic Relational Models

Evidence often grounds temporal probabilistic relational models over time, which makes reasoning infeasible. To counteract groundings over time and to keep reasoning polynomial by restoring a lifted representation, we present temporal approximate merging (TAMe), which incorporates (i) clustering for grouping submodels as well as (ii) statistical significance checks to test the fitness of the clustering outcome. In exchange for faster runtimes, TAMe introduces a bounded error that becomes negligible over time. Empirical results show that TAMe significantly improves the runtime performance of inference, while keeping errors small.

Answering Hindsight Queries with Lifted Dynamic Junction Trees

The lifted dynamic junction tree algorithm (LDJT) efficiently answers filtering and prediction queries for probabilistic relational temporal models by building and then reusing a first-order cluster representation of a knowledge base for multiple queries and time steps. We extend LDJT to (i) solve the smoothing inference problem to answer hindsight queries by introducing an efficient backward pass and (ii) discuss different options to instantiate a first-order cluster representation during a backward pass. Further, our relational forward backward algorithm makes hindsight queries to the very beginning feasible. LDJT answers multiple temporal queries faster than the static lifted junction tree algorithm on an unrolled model, which performs smoothing during message passing.

Preventing Unnecessary Groundings in the Lifted Dynamic Junction Tree Algorithm

The lifted dynamic junction tree algorithm (LDJT) efficiently answers filtering and prediction queries for probabilistic relational temporal models by building and then reusing a first-order cluster representation of a knowledge base for multiple queries and time steps. Unfortunately, a non-ideal elimination order can lead to groundings even though a lifted run is possible for a model. We extend LDJT (i) to identify unnecessary groundings while proceeding in time and (ii) to prevent groundings by delaying eliminations through changes in a temporal first-order cluster representation. The extended version of LDJT answers multiple temporal queries orders of magnitude faster than the original version.

Fusing First-order Knowledge Compilation and the Lifted Junction Tree Algorithm

Standard approaches for inference in probabilistic formalisms with first-order constructs include lifted variable elimination (LVE) for single queries as well as first-order knowledge compilation (FOKC) based on weighted model counting. To handle multiple queries efficiently, the lifted junction tree algorithm (LJT) uses a first-order cluster representation of a model and LVE as a subroutine in its computations. For certain inputs, the implementations of LVE and, as a result, LJT ground parts of a model where FOKC has a lifted run. The purpose of this paper is to prepare LJT as a backbone for lifted inference and to use any exact inference algorithm as subroutine. Using FOKC in LJT allows us to compute answers faster than LJT, LVE, and FOKC for certain inputs.