Denoising the Future: Top-p Distributions for Moving Through Time

Inference in dynamic probabilistic models is a complex task involving expensive operations. In particular, for Hidden Markov Models, the whole state space has to be enumerated for advancing in time. Even states with negligible probabilities are considered, resulting in computational inefficiency and increased noise due to the propagation of unlikely probability mass. We propose to denoise the future and speed up inference by using only the top-p states, i.e., the most probable states with accumulated probability p. We show that the error introduced by using only the top-p states is bound by p and the so-called minimal mixing rate of the underlying model. Moreover, in our empirical evaluation, we show that we can expect speedups of at least an order of magnitude, while the error in terms of total variation distance is below 0.09.

Compression versus Accuracy: A Hierarchy of Lifted Models

Probabilistic graphical models that encode indistinguishable objects and relations among them use first-order logic constructs to compress a propositional factorised model for more efficient (lifted) inference. To obtain a lifted representation, the state-of-the-art algorithm Advanced Colour Passing (ACP) groups factors that represent matching distributions. In an approximate version using $\varepsilon$ as a hyperparameter, factors are grouped that differ by a factor of at most $(1\pm \varepsilon)$. However, finding a suitable $\varepsilon$ is not obvious and may need a lot of exploration, possibly requiring many ACP runs with different $\varepsilon$ values. Additionally, varying $\varepsilon$ can yield wildly different models, leading to decreased interpretability. Therefore, this paper presents a hierarchical approach to lifted model construction that is hyperparameter-free. It efficiently computes a hierarchy of $\varepsilon$ values that ensures a hierarchy of models, meaning that once factors are grouped together given some $\varepsilon$, these factors will be grouped together for larger $\varepsilon$ as well. The hierarchy of $\varepsilon$ values also leads to a hierarchy of error bounds. This allows for explicitly weighing compression versus accuracy when choosing specific $\varepsilon$ values to run ACP with and enables interpretability between the different models.

Lifted Forward Planning in Relational Factored Markov Decision Processes with Concurrent Actions

Decision making is a central problem in AI that can be formalized using a Markov Decision Process. A problem is that, with increasing numbers of (indistinguishable) objects, the state space grows exponentially. To compute policies, the state space has to be enumerated. Even more possibilities have to be enumerated if the size of the action space depends on the size of the state space, especially if we allow concurrent actions. To tackle the exponential blow-up in the action and state space, we present a first-order representation to store the spaces in polynomial instead of exponential size in the number of objects and introduce Foreplan, a relational forward planner, which uses this representation to efficiently compute policies for numerous indistinguishable objects and actions. Additionally, we introduce an even faster approximate version of Foreplan. Moreover, Foreplan identifies how many objects an agent should act on to achieve a certain task given restrictions. Further, we provide a theoretical analysis and an empirical evaluation of Foreplan, demonstrating a speedup of at least four orders of magnitude.

Approximate Lifted Model Construction

Probabilistic relational models such as parametric factor graphs enable efficient (lifted) inference by exploiting the indistinguishability of objects. In lifted inference, a representative of indistinguishable objects is used for computations. To obtain a relational (i.e., lifted) representation, the Advanced Colour Passing (ACP) algorithm is the state of the art. The ACP algorithm, however, requires underlying distributions, encoded as potential-based factorisations, to exactly match to identify and exploit indistinguishabilities. Hence, ACP is unsuitable for practical applications where potentials learned from data inevitably deviate even if associated objects are indistinguishable. To mitigate this problem, we introduce the $\varepsilon$-Advanced Colour Passing ($\varepsilon$-ACP) algorithm, which allows for a deviation of potentials depending on a hyperparameter $\varepsilon$. $\varepsilon$-ACP efficiently uncovers and exploits indistinguishabilities that are not exact. We prove that the approximation error induced by $\varepsilon$-ACP is strictly bounded and our experiments show that the approximation error is close to zero in practice.

Lifted Model Construction without Normalisation: A Vectorised Approach to Exploit Symmetries in Factor Graphs

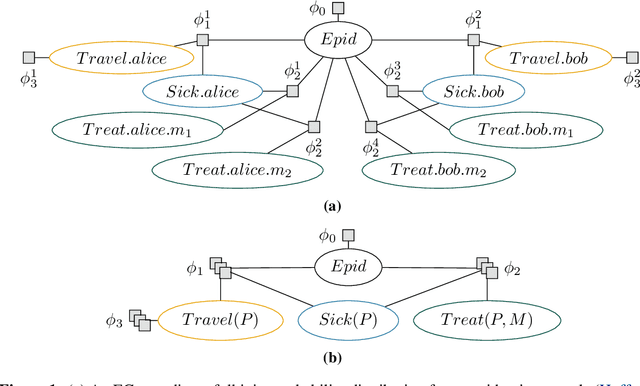
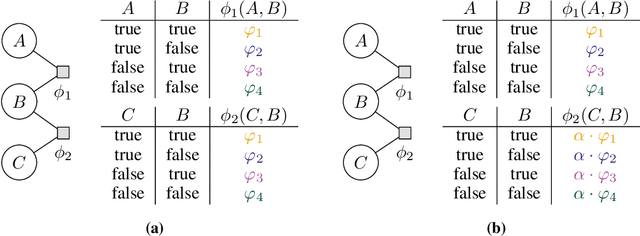
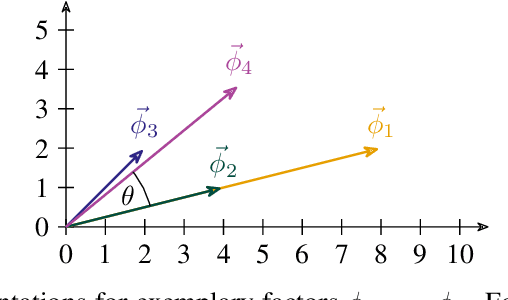
Lifted probabilistic inference exploits symmetries in a probabilistic model to allow for tractable probabilistic inference with respect to domain sizes of logical variables. We found that the current state-of-the-art algorithm to construct a lifted representation in form of a parametric factor graph misses symmetries between factors that are exchangeable but scaled differently, thereby leading to a less compact representation. In this paper, we propose a generalisation of the advanced colour passing (ACP) algorithm, which is the state of the art to construct a parametric factor graph. Our proposed algorithm allows for potentials of factors to be scaled arbitrarily and efficiently detects more symmetries than the original ACP algorithm. By detecting strictly more symmetries than ACP, our algorithm significantly reduces online query times for probabilistic inference when the resulting model is applied, which we also confirm in our experiments.

Estimating Causal Effects in Partially Directed Parametric Causal Factor Graphs

Lifting uses a representative of indistinguishable individuals to exploit symmetries in probabilistic relational models, denoted as parametric factor graphs, to speed up inference while maintaining exact answers. In this paper, we show how lifting can be applied to causal inference in partially directed graphs, i.e., graphs that contain both directed and undirected edges to represent causal relationships between random variables. We present partially directed parametric causal factor graphs (PPCFGs) as a generalisation of previously introduced parametric causal factor graphs, which require a fully directed graph. We further show how causal inference can be performed on a lifted level in PPCFGs, thereby extending the applicability of lifted causal inference to a broader range of models requiring less prior knowledge about causal relationships.

Efficient Detection of Commutative Factors in Factor Graphs

Lifted probabilistic inference exploits symmetries in probabilistic graphical models to allow for tractable probabilistic inference with respect to domain sizes. To exploit symmetries in, e.g., factor graphs, it is crucial to identify commutative factors, i.e., factors having symmetries within themselves due to their arguments being exchangeable. The current state of the art to check whether a factor is commutative with respect to a subset of its arguments iterates over all possible subsets of the factor's arguments, i.e., $O(2^n)$ iterations for a factor with $n$ arguments in the worst case. In this paper, we efficiently solve the problem of detecting commutative factors in a factor graph. In particular, we introduce the detection of commutative factors (DECOR) algorithm, which allows us to drastically reduce the computational effort for checking whether a factor is commutative in practice. We prove that DECOR efficiently identifies restrictions to drastically reduce the number of required iterations and validate the efficiency of DECOR in our empirical evaluation.

Lifting Factor Graphs with Some Unknown Factors

Lifting exploits symmetries in probabilistic graphical models by using a representative for indistinguishable objects, allowing to carry out query answering more efficiently while maintaining exact answers. In this paper, we investigate how lifting enables us to perform probabilistic inference for factor graphs containing factors whose potentials are unknown. We introduce the Lifting Factor Graphs with Some Unknown Factors (LIFAGU) algorithm to identify symmetric subgraphs in a factor graph containing unknown factors, thereby enabling the transfer of known potentials to unknown potentials to ensure a well-defined semantics and allow for (lifted) probabilistic inference.

Efficient Detection of Exchangeable Factors in Factor Graphs

To allow for tractable probabilistic inference with respect to domain sizes, lifted probabilistic inference exploits symmetries in probabilistic graphical models. However, checking whether two factors encode equivalent semantics and hence are exchangeable is computationally expensive. In this paper, we efficiently solve the problem of detecting exchangeable factors in a factor graph. In particular, we introduce the detection of exchangeable factors (DEFT) algorithm, which allows us to drastically reduce the computational effort for checking whether two factors are exchangeable in practice. While previous approaches iterate all $O(n!)$ permutations of a factor's argument list in the worst case (where $n$ is the number of arguments of the factor), we prove that DEFT efficiently identifies restrictions to drastically reduce the number of permutations and validate the efficiency of DEFT in our empirical evaluation.

Lifted Causal Inference in Relational Domains

Lifted inference exploits symmetries in probabilistic graphical models by using a representative for indistinguishable objects, thereby speeding up query answering while maintaining exact answers. Even though lifting is a well-established technique for the task of probabilistic inference in relational domains, it has not yet been applied to the task of causal inference. In this paper, we show how lifting can be applied to efficiently compute causal effects in relational domains. More specifically, we introduce parametric causal factor graphs as an extension of parametric factor graphs incorporating causal knowledge and give a formal semantics of interventions therein. We further present the lifted causal inference algorithm to compute causal effects on a lifted level, thereby drastically speeding up causal inference compared to propositional inference, e.g., in causal Bayesian networks. In our empirical evaluation, we demonstrate the effectiveness of our approach.