Lifted Model Construction without Normalisation: A Vectorised Approach to Exploit Symmetries in Factor Graphs
Paper and Code
Nov 20, 2024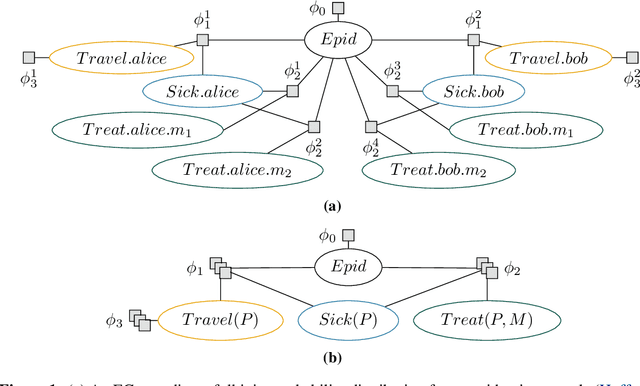
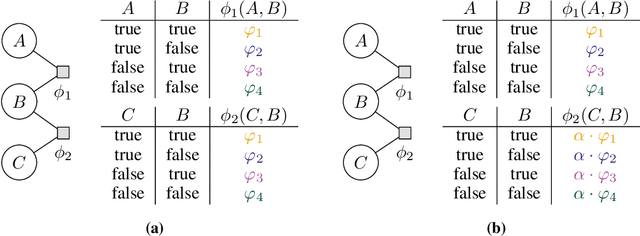
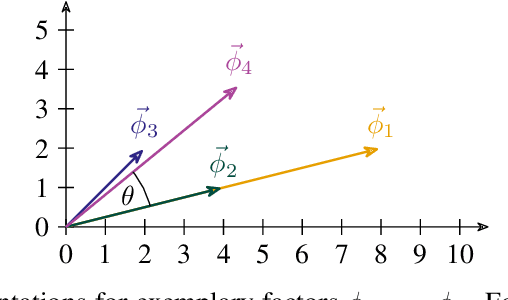

Lifted probabilistic inference exploits symmetries in a probabilistic model to allow for tractable probabilistic inference with respect to domain sizes of logical variables. We found that the current state-of-the-art algorithm to construct a lifted representation in form of a parametric factor graph misses symmetries between factors that are exchangeable but scaled differently, thereby leading to a less compact representation. In this paper, we propose a generalisation of the advanced colour passing (ACP) algorithm, which is the state of the art to construct a parametric factor graph. Our proposed algorithm allows for potentials of factors to be scaled arbitrarily and efficiently detects more symmetries than the original ACP algorithm. By detecting strictly more symmetries than ACP, our algorithm significantly reduces online query times for probabilistic inference when the resulting model is applied, which we also confirm in our experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge