Statistical and Algorithmic Insights for Semi-supervised Learning with Self-training

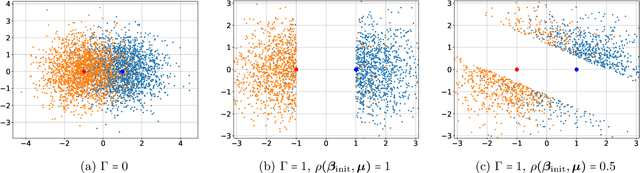
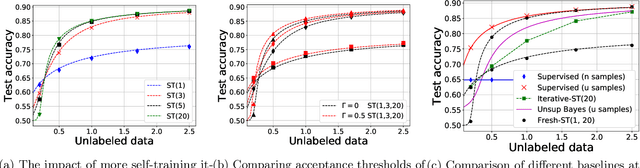
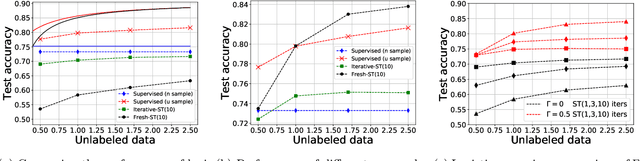
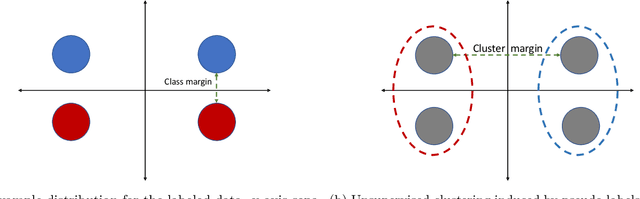
Self-training is a classical approach in semi-supervised learning which is successfully applied to a variety of machine learning problems. Self-training algorithm generates pseudo-labels for the unlabeled examples and progressively refines these pseudo-labels which hopefully coincides with the actual labels. This work provides theoretical insights into self-training algorithm with a focus on linear classifiers. We first investigate Gaussian mixture models and provide a sharp non-asymptotic finite-sample characterization of the self-training iterations. Our analysis reveals the provable benefits of rejecting samples with low confidence and demonstrates that self-training iterations gracefully improve the model accuracy even if they do get stuck in sub-optimal fixed points. We then demonstrate that regularization and class margin (i.e. separation) is provably important for the success and lack of regularization may prevent self-training from identifying the core features in the data. Finally, we discuss statistical aspects of empirical risk minimization with self-training for general distributions. We show how a purely unsupervised notion of generalization based on self-training based clustering can be formalized based on cluster margin. We then establish a connection between self-training based semi-supervision and the more general problem of learning with heterogenous data and weak supervision.

Stronger Convergence Results for Deep Residual Networks: Network Width Scales Linearly with Training Data Size

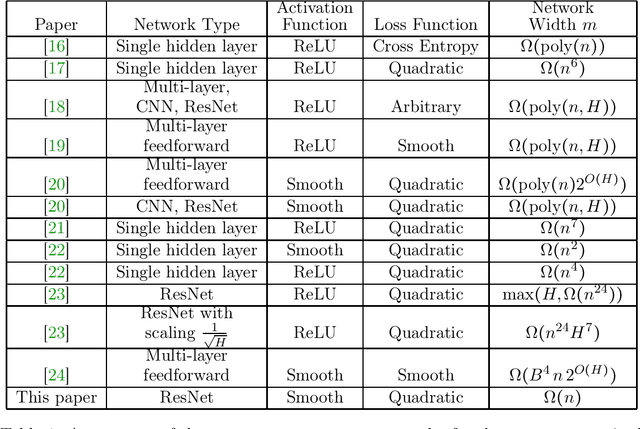
Deep neural networks are highly expressive machine learning models with the ability to interpolate arbitrary datasets. Deep nets are typically optimized via first-order methods and the optimization process crucially depends on the characteristics of the network as well as the dataset. This work sheds light on the relation between the network size and the properties of the dataset with an emphasis on deep residual networks (ResNets). Our contribution is that if the network Jacobian is full rank, gradient descent for the quadratic loss and smooth activation converges to the global minima even if the network width $m$ of the ResNet scales linearly with the sample size $n$, and independently from the network depth. To the best of our knowledge, this is the first work which provides a theoretical guarantee for the convergence of neural networks in the $m=\Omega(n)$ regime.

Comments on "Deep Neural Networks with Random Gaussian Weights: A Universal Classification Strategy?"

In a recently published paper [1], it is shown that deep neural networks (DNNs) with random Gaussian weights preserve the metric structure of the data, with the property that the distance shrinks more when the angle between the two data points is smaller. We agree that the random projection setup considered in [1] preserves distances with a high probability. But as far as we are concerned, the relation between the angle of the data points and the output distances is quite the opposite, i.e., smaller angles result in a weaker distance shrinkage. This leads us to conclude that Theorem 3 and Figure 5 in [1] are not accurate. Hence the usage of random Gaussian weights in DNNs cannot provide an ability of universal classification or treating in-class and out-of-class data separately. Consequently, the behavior of networks consisting of random Gaussian weights only is not useful to explain how DNNs achieve state-of-art results in a large variety of problems.